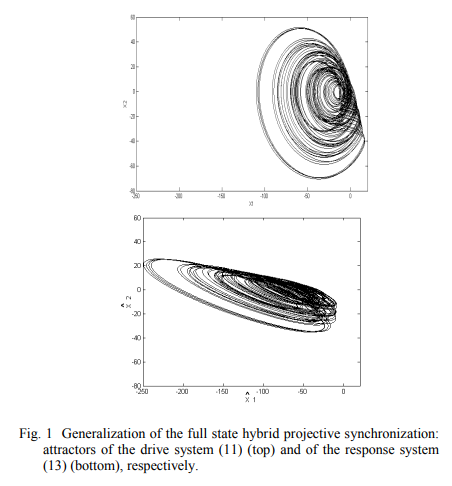
Chaos synchronisation of continuous systems via scalar signal
By analyzing the issue of chaos synchronization in the literature, it can be noticed the lack of a general approach, which would enable any type of synchronization to be achieved. Similarly, there is the lack of a unified method for synchronizing both continuous-time and discrete-time systems via a scalar signal. This paper and the companion one [1] aim to bridge these two gaps by presenting a novel general unified framework to synchronize chaotic systems via a scalar signal. The framework, based on the concept of observer, enables any type of synchronization defined to date to be achieved for
Circuit Theory and Applications
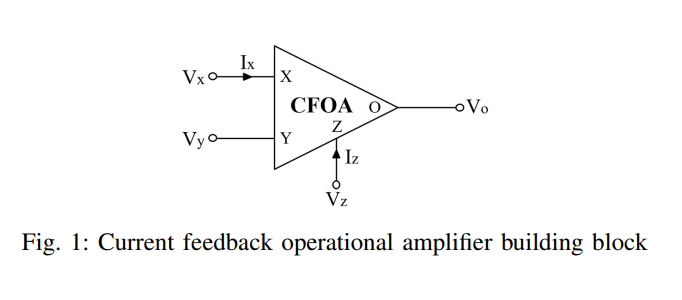
On the realization of Current-Mode Fractional-order Simulated Inductors
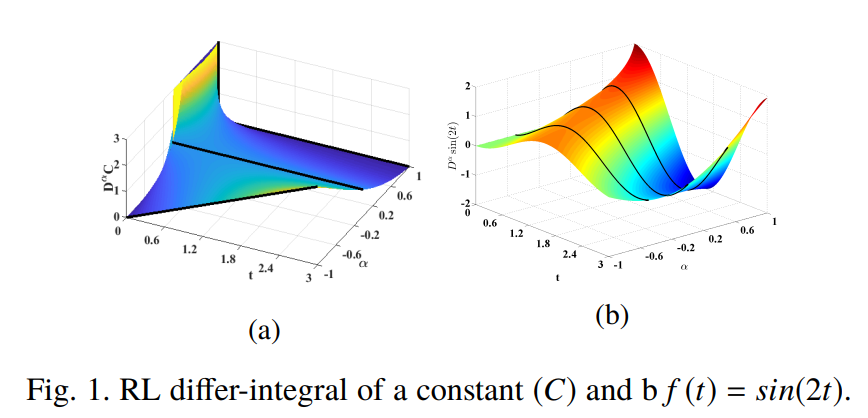
Fractional calculus definitions, approximations, and engineering applications
The basic idea behind fractional calculus is that it considers derivatives and integrals of non-integer orders giving extra degrees of freedom and tuning knobs for modeling complex and memory dependent systems with compact descriptions. This paper reviews fractional calculus history, theory, and its applications in electrical engineering. The basic definitions of fractional calculus are presented together with some examples. Integer order transfer function approximations and constant phase elements (CPEs) emulators are overviewed due to their importance in implementing fractional-order
Circuit Theory and Applications
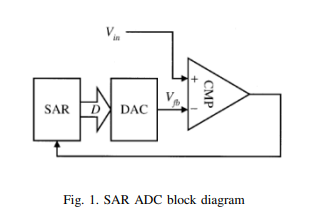
A 26.24uW 9.26-ENOB Dynamic RAM Based SAR ADC for Biomedical Applications
This work introduces a new successive approximation register circuit (SAR) for SAR analog to digital converter (ADC) based on Dynamic Random Access Memory (DRAM) cells. Based on the proposed DRAM based SAR ADC and a differential capacitive DAC, a 10-bit 2V ADC is designed in 0.18um CMOS technology. The proposed SAR is compared to traditional SAR to verify that the proposed SAR decreases the power of SAR ADC for biomedical applications. The power consumption for the proposed SAR ADC is found to be 26.24uW with ENOB equal to 9.26, and the maximum sampling frequency is 1MHz. For the traditional
