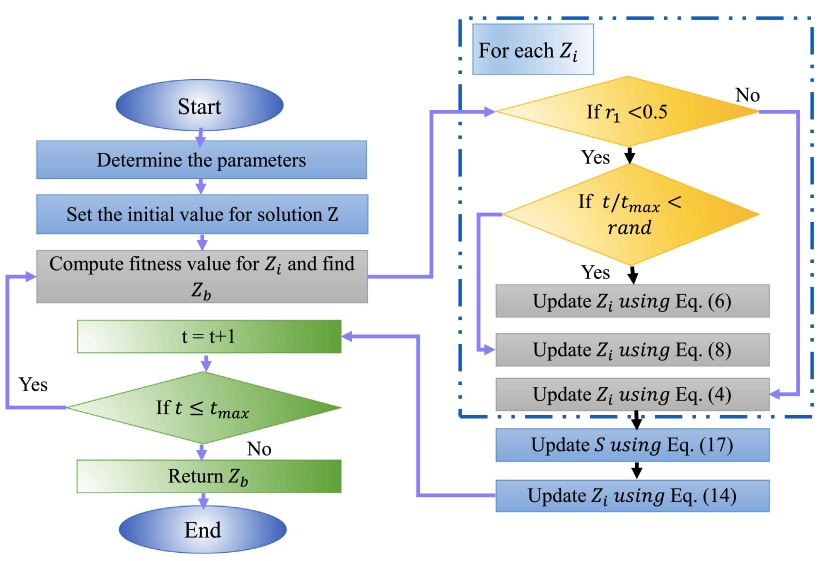
A Grunwald–Letnikov based Manta ray foraging optimizer for global optimization and image segmentation
This paper presents a modified version of Manta ray foraging optimizer (MRFO) algorithm to deal with global optimization and multilevel image segmentation problems. MRFO is a meta-heuristic technique that simulates the behaviors of manta rays to find the food. MRFO established its ability to find a suitable solution for a variant of optimization problems. However, by analyzing its behaviors during the optimization process, it is observed that its exploitation ability is less than exploration ability, which makes MRFO more sensitive to attractive to a local point. Therefore, we enhanced MRFO by
Atmospheric pressure air microplasma current time series for true random bit generation
Generating true random bits of high quality at high data rates is usually viewed as a challenging task. To do so, physical sources of entropy with wide bandwidth are required which are able to provide truly random bits and not pseudorandom bits, as it is the case with deterministic algorithms and chaotic systems. In this work we demonstrate a reliable high-speed true random bit generator (TRBG) device based on the unpredictable electrical current time series of atmospheric pressure air microplasma (APAMP). After binarization of the sampled current time series, no further post-processing was
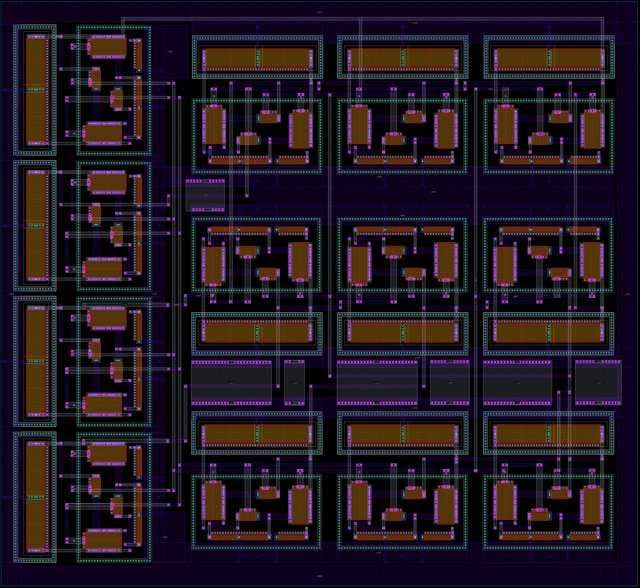
Design of low-voltage FO-[PD] controller for motion systems
Fractional-order controllers have gained significant research interest in various practical applications due to the additional degrees of freedom offered in their tuning process. The main contribution of this work is the analog implementation, for the first time in the literature, of a fractional-order controller with a transfer function that is not directly constructed from terms of the fractional-order Laplacian operator. This is achieved using Padé approximation, and the resulting integer-order transfer function is implemented using operational transconductance amplifiers as active elements
Fractional derivative modeling of double-diffusive free convection with von Neumann stability analysis
This paper focuses on the problem of fractional time derivative of fluid flow and convective heat and mass transfer from a heated semi-infinite wall immersed. We provided two cases of study, one is free convective heat transfer and the other is a free double-convective heat and mass transfer. The time-derivative terms in the equations of momentum, energy and concentration are assumed to be fractional using the Grunwald-Letnikov (GL) model. A finite difference scheme has been developed for each case of study and followed by a von Neumann stability analysis. Therefore, a stability condition has
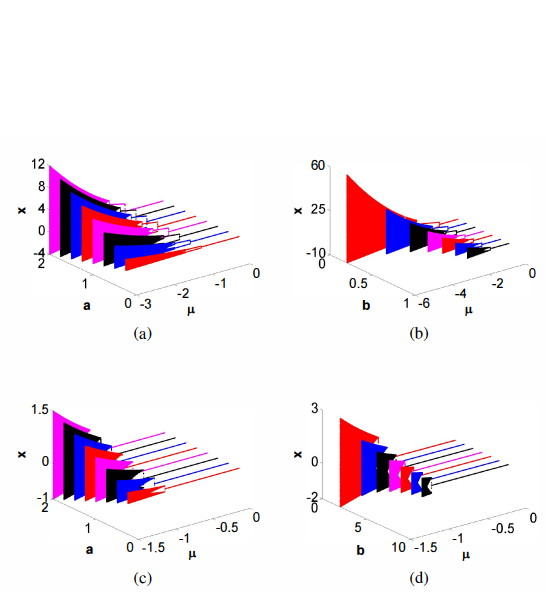
Design of a generalized bidirectional tent map suitable for encryption applications
The discrete tent map is one of the most famous discrete chaotic maps that has widely-spread applications. This paper investigates a set of four generalized tent maps where the conventional map is a special case. The proposed maps have extra degrees of freedom which provide different chaotic characteristics and increase the design flexibility required for many applications. Mathematical analyses for generalized positive and mostly positive tent maps include: bifurcation diagrams relative to all parameters, effective range of parameters, bifurcation points. The maximum Lyapunov exponent (MLE)
Controlled Picard Method for Solving Nonlinear Fractional Reaction–Diffusion Models in Porous Catalysts
This paper discusses the diffusion and reaction behaviors of catalyst pellets in the fractional-order domain as well as the case of nth-order reactions. Two generic models are studied to calculate the concentration of reactant in a porous catalyst in the case of a spherical geometric pellet and a flat-plate particle with different examples. A controlled Picard analytical method is introduced to obtain an approximated solution for these systems in both linear and nonlinear cases. This method can cover a wider range of problems due to the extra auxiliary parameter, which enhances the convergence
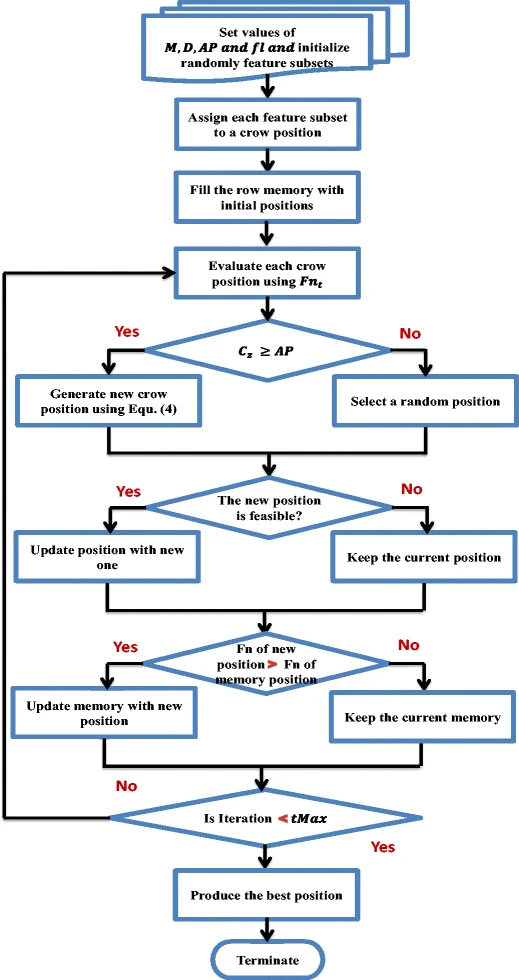
Feature selection via a novel chaotic crow search algorithm
Crow search algorithm (CSA) is a new natural inspired algorithm proposed by Askarzadeh in 2016. The main inspiration of CSA came from crow search mechanism for hiding their food. Like most of the optimization algorithms, CSA suffers from low convergence rate and entrapment in local optima. In this paper, a novel meta-heuristic optimizer, namely chaotic crow search algorithm (CCSA), is proposed to overcome these problems. The proposed CCSA is applied to optimize feature selection problem for 20 benchmark datasets. Ten chaotic maps are employed during the optimization process of CSA. The
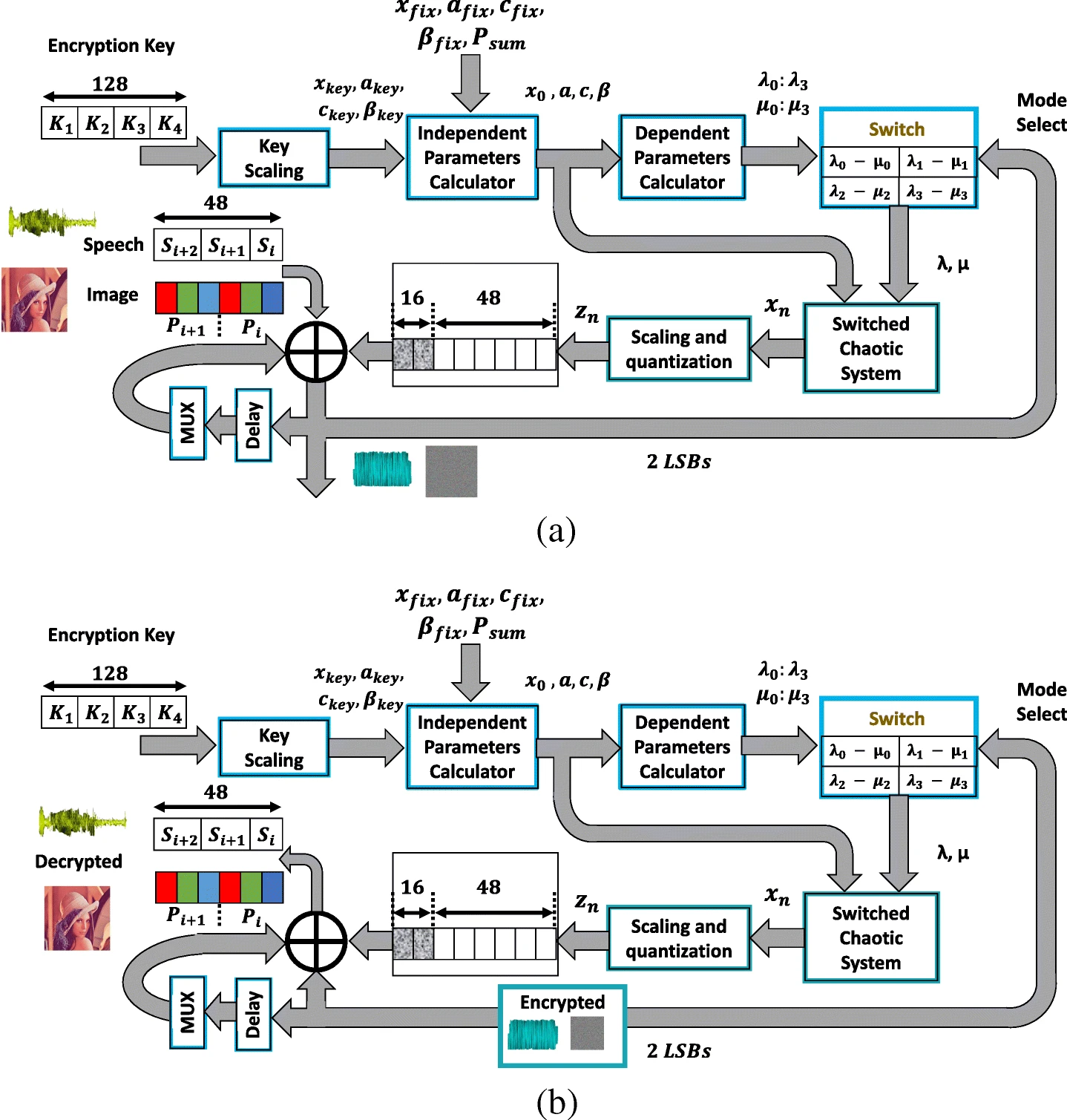
A switched chaotic encryption scheme using multi-mode generalized modified transition map
This paper presents a multi-mode generalized modified transition chaotic map and a switched chaotic encryption scheme based on it. Eight different modes of operation can be selected based on the map graph (concave or convex), the range modification procedure (shrinking or widening) and the sign of one of its independent parameters. The generalization and modification preserve the controllability and continuous chaotic behavior properties, respectively. For the same encryption key and map equation, multi-mode operation occurs through switching between four alternatives of the dependent
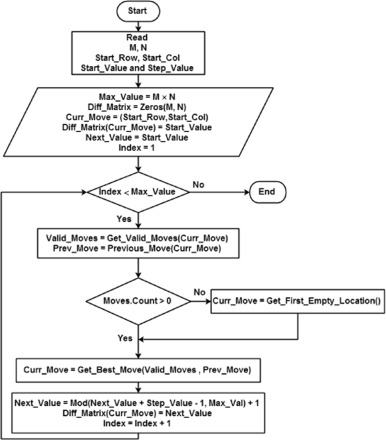
Novel permutation measures for image encryption algorithms
This paper proposes two measures for the evaluation of permutation techniques used in image encryption. First, a general mathematical framework for describing the permutation phase used in image encryption is presented. Using this framework, six different permutation techniques, based on chaotic and non-chaotic generators, are described. The two new measures are, then, introduced to evaluate the effectiveness of permutation techniques. These measures are (1) Percentage of Adjacent Pixels Count (PAPC) and (2) Distance Between Adjacent Pixels (DBAP). The proposed measures are used to evaluate
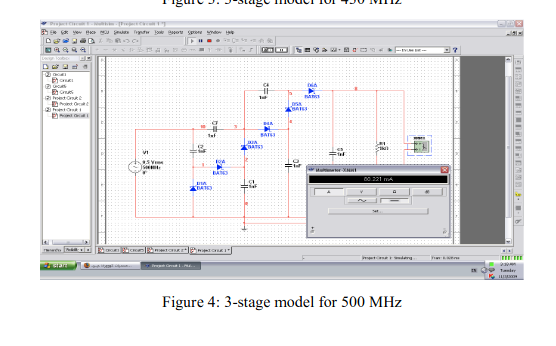
Novel radio frequency energy harvesting model
Energy and Environment, both are the main concern for every researcher allover the world. Alternative energy sources that are environmental friendly became the challenge to satisfy world needs. Oil and Gas are no more the main source of Energy, consequently the demand of an everlasting cheap source of energy that is environmental friendly, is the main goal recently. During the last decade, power consumption has decreased opening the field for energy harvesting to become a real time solution for providing different sources of electrical power. Energy Harvesting is a new technology that is going
Pagination
- Previous page ‹‹
- Page 33
- Next page ››
