Fractional-order mutual inductance: Analysis and design
This paper introduces for the first time the generalized concept of the mutual inductance in the fractional-order domain where the symmetrical and unsymmetrical behaviors of the fractional-order mutual inductance are studied. To use the fractional mutual inductance in circuit design and simulation, an equivalent circuit is presented with its different conditions of operation. Also, simulations for the impedance matrix parameters of the fractional mutual inductance equivalent circuit using Advanced Design System and MATLAB are illustrated. The Advanced Design System and MATLAB simulations of
FPGA realizations of high-speed switching-type chaotic oscillators using compact VHDL codes
This paper introduces high-speed FPGA implementations of two different chaotic systems that rely on a switching-type nonlinearity. In particular, the single-switch Jerk system and the two-wing butterfly system (previously implemented only in analog form) are realized on a modular FPGA platform. For each system, two different hardware architectures are described: a parameters-independent architecture and a customized one with fixed parameters that utilizes less FPGA resources and thus has high throughput with the minimum number of clock cycles. Experimental results show that the parameters
Single active element implementation of fractional-order differentiators and integrators
A novel topology for implementing fractional-order differentiator and integrator transfer functions is presented in this paper. This topology is based on the employment of a second generation Current Conveyor with EXtra inputs (EX-CCII), passive resistors, and fractional-order capacitors. The main benefit offered by this implementation is that both fractional-order differentiator and integrator transfer functions are simultaneously available at different output terminals, and that their frequency characteristics can be orthogonally adjusted without disturbing each other. With only one EX-CCII
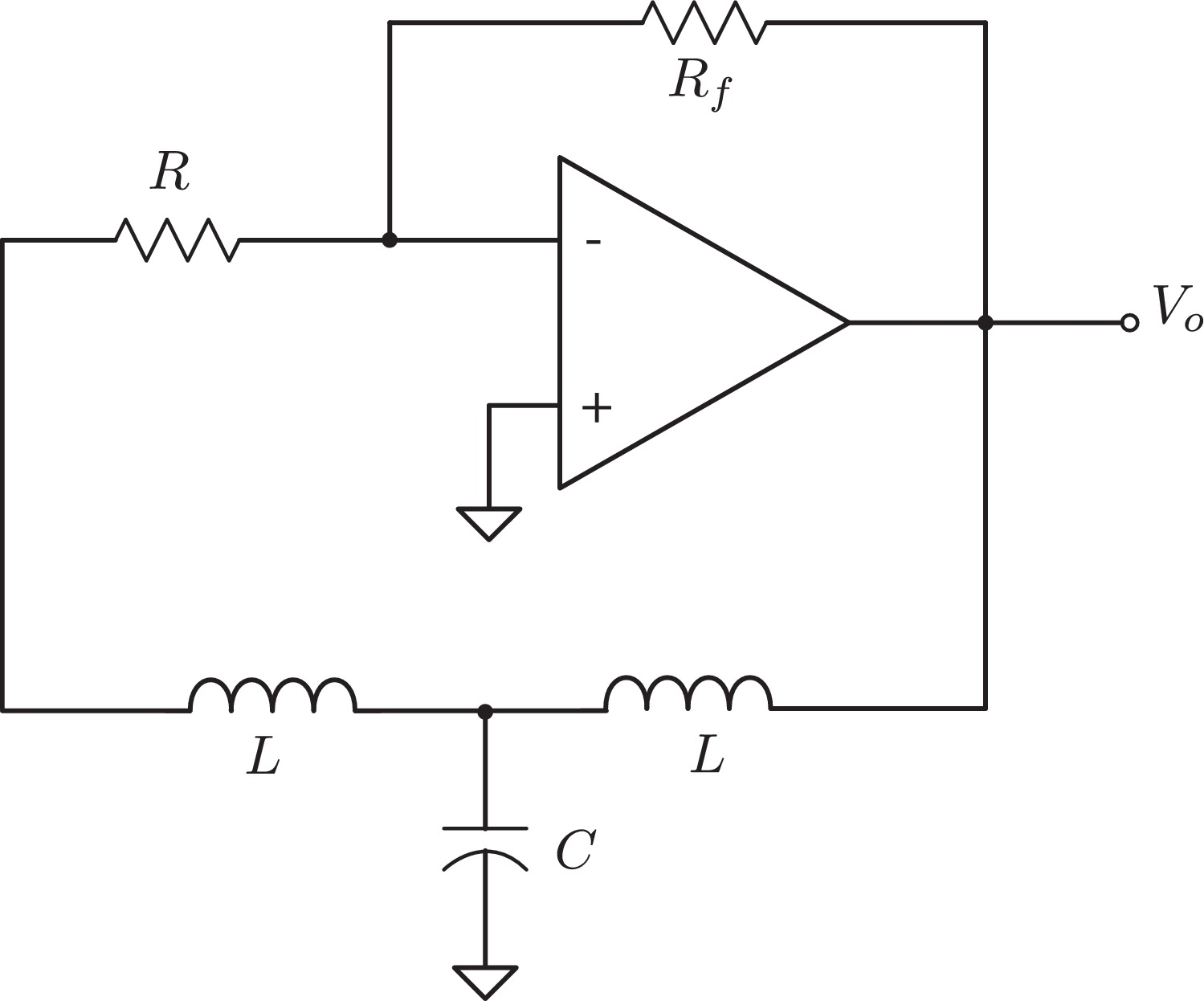
Fractional Order Sallen–Key and KHN Filters: Stability and Poles Allocation
This paper presents the analysis for allocating the system poles and hence controlling the system stability for KHN and Sallen–Key fractional order filters. The stability analysis and stability contours for two different fractional order transfer functions with two different fractional order elements are presented. The effect of the transfer function parameters on the singularities of the system is demonstrated where the number of poles becomes dependent on the transfer function parameters as well as the fractional orders. Numerical, circuit simulation, and experimental work are used in the
Experimental demonstration of fractional-order oscillators of orders 2.6 and 2.7
The purpose of this work is to provide an experimental demonstration for the development of sinusoidal oscillations in a fractional-order Hartley-like oscillator. Solid-state fractional-order electric double-layer capacitors were first fabricated using graphene-percolated P(VDF-TrFE-CFE) composite structure, and then characterized by using electrochemical impedance spectroscopy. The devices exhibit the fractional orders of 0.6 and 0.74 respectively (using the model Zc=Rs+1/(jω)αCα), with the corresponding pseudocapacitances of approximately 93nFsec−0.4 and 1.5nFsec−0.26 over the frequency
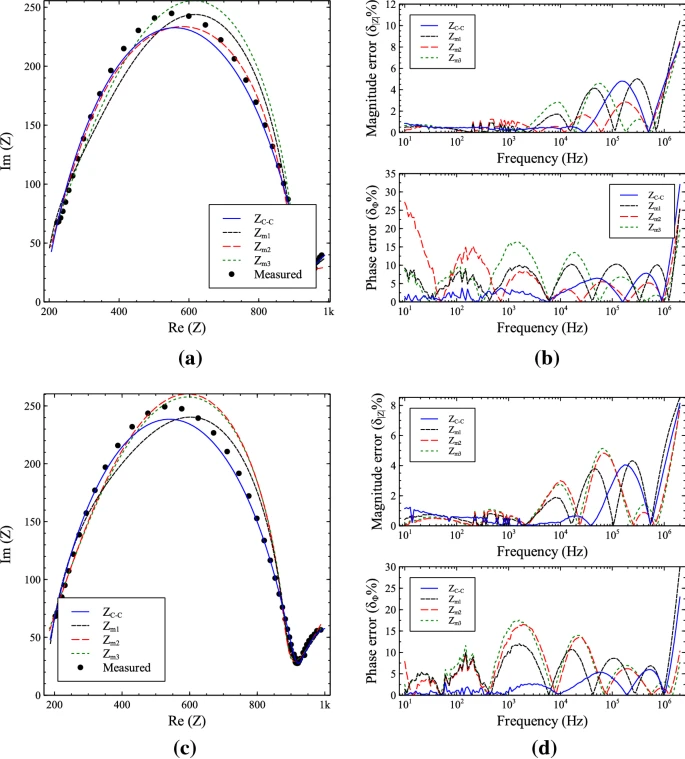
Novel Double-Dispersion Models Based on Power-Law Filters
Novel double-dispersion models based on power-law filters are introduced in this work. These models are based on standard first-order and/or second-order low-pass filter transfer functions (denoted as mother functions) and do not require the employment of the fractional-order Laplacian operator. An attractive benefit, from the flexibility point of view, is that the number of parameters, which must be determined via optimization routines, depends on the selected combinations of mother filters. The validity of the proposed models is verified through fitting experimental bio-impedance data of
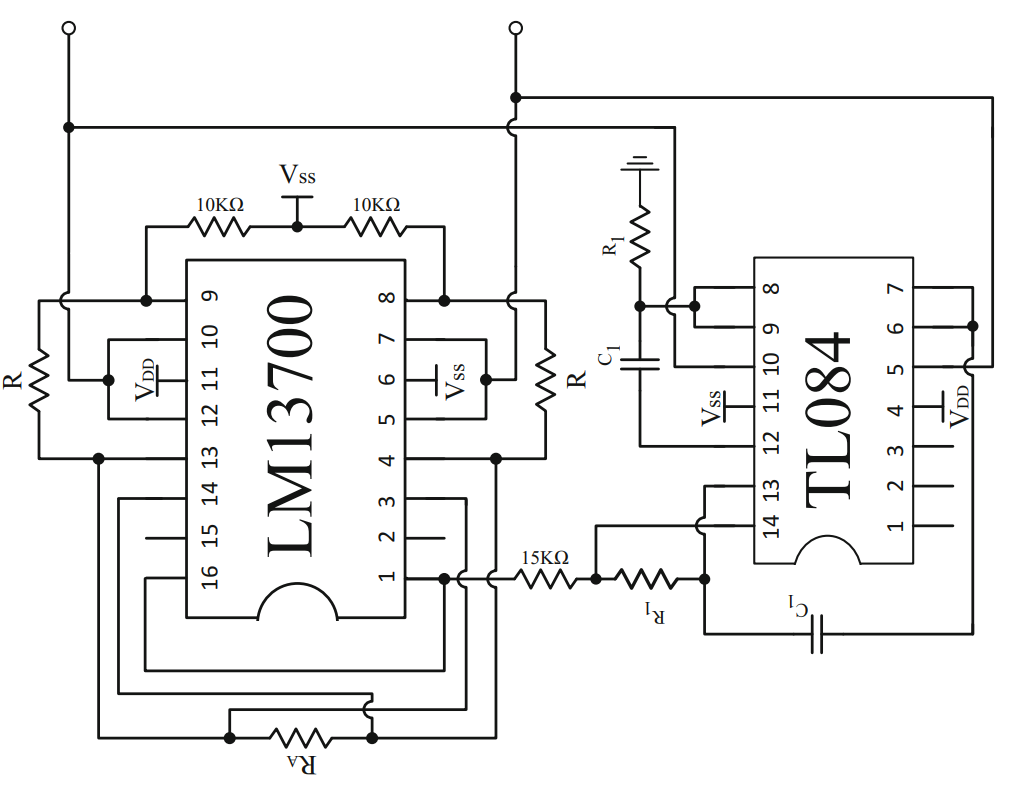
Simple MOS-based circuit designed to show pinched hysteresis behavior
We propose and validate a simple 3-transistor MOS circuit that shows an all-positive pinched hysteresis behavior. Complete analysis of the circuit is provided along with experimental results using a commercial CMOS transistor array. Copyright © 2018 John Wiley & Sons, Ltd.
Memristor and inverse memristor: Modeling, implementation and experiments
Pinched hysteresis is considered to be a signature of the existence of memristive behavior. However, this is not completely accurate. In this chapter, we are discussing a general equation taking into consideration all possible cases to model all known elements including memristor. Based on this equation, it is found that an opposite behavior to the memristor can exist in a nonlinear inductor or a nonlinear capacitor (both with quadratic nonlinearity) or a derivative-controlled nonlinear resistor/transconductor which we refer to as the inverse memristor. We discuss the behavior of this new
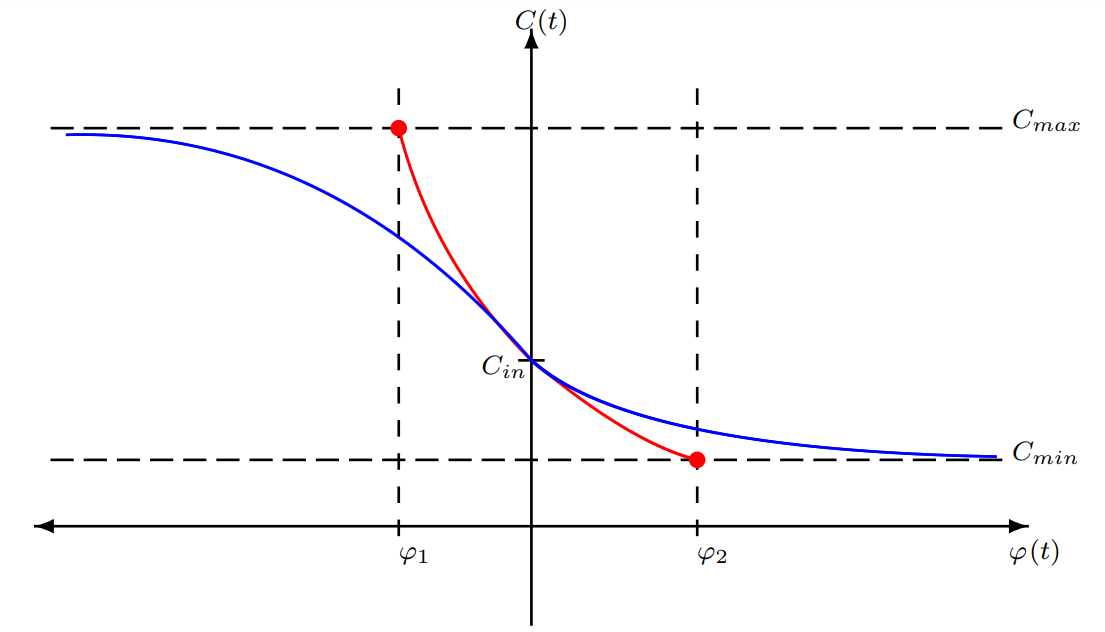
Boundary Dynamics of Memcapacitor in Voltage-Excited Circuits and Relaxation Oscillators
This paper discusses the boundary dynamics of the charge-controlled memcapacitor for Joglekar’s window function that describes the nonlinearities of the memcapacitor’s boundaries. A closed form solution for the memcapacitance is introduced for general doping factor (Formula presented.)p. The derived formulas are used to predict the behavior of the memcapacitor under different voltage excitation sources showing a great matching with the circuit simulations. The effect of the doping factor (Formula presented.) on the time domain response of the memcapacitor has been studied as compared to the
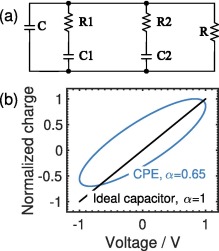
Nonlinear charge-voltage relationship in constant phase element
The constant phase element (CPE) or fractional-order capacitor is an electrical device that has an impedance of the form Z(s)=1/Cαsα, where Cα is the CPE parameter and α is a fractional dispersion coefficient of values between 0 and 1. Here we show that in the time-domain the classical linear charge-voltage relationship of ideal capacitors, q=C·v, is not valid for CPEs. In fact the relationship is nonlinear and can be expressed as q=C(v;Cα,α)·v. We verify our findings using (i) circuit simulations of an integer-order emulator of a CPE, and (ii) experimental results from a commercial
Pagination
- Previous page ‹‹
- Page 32
- Next page ››
