Fractional derivative modeling of double-diffusive free convection with von Neumann stability analysis
This paper focuses on the problem of fractional time derivative of fluid flow and convective heat and mass transfer from a heated semi-infinite wall immersed. We provided two cases of study, one is free convective heat transfer and the other is a free double-convective heat and mass transfer. The time-derivative terms in the equations of momentum, energy and concentration are assumed to be fractional using the Grunwald-Letnikov (GL) model. A finite difference scheme has been developed for each case of study and followed by a von Neumann stability analysis. Therefore, a stability condition has
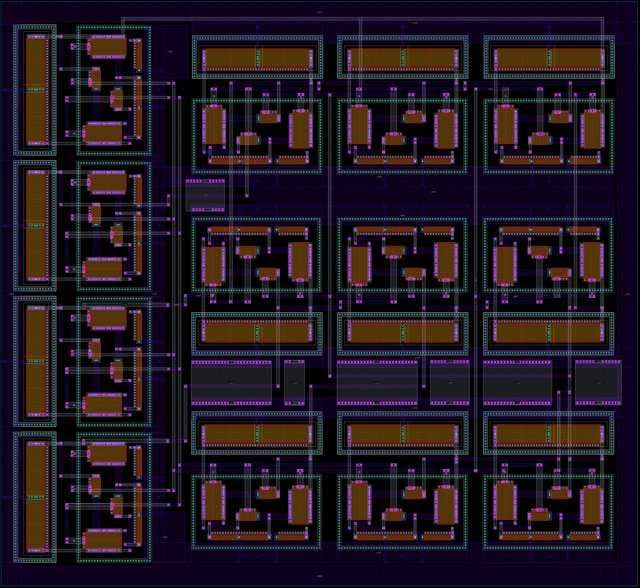
Design of low-voltage FO-[PD] controller for motion systems
Fractional-order controllers have gained significant research interest in various practical applications due to the additional degrees of freedom offered in their tuning process. The main contribution of this work is the analog implementation, for the first time in the literature, of a fractional-order controller with a transfer function that is not directly constructed from terms of the fractional-order Laplacian operator. This is achieved using Padé approximation, and the resulting integer-order transfer function is implemented using operational transconductance amplifiers as active elements
Atmospheric pressure air microplasma current time series for true random bit generation
Generating true random bits of high quality at high data rates is usually viewed as a challenging task. To do so, physical sources of entropy with wide bandwidth are required which are able to provide truly random bits and not pseudorandom bits, as it is the case with deterministic algorithms and chaotic systems. In this work we demonstrate a reliable high-speed true random bit generator (TRBG) device based on the unpredictable electrical current time series of atmospheric pressure air microplasma (APAMP). After binarization of the sampled current time series, no further post-processing was
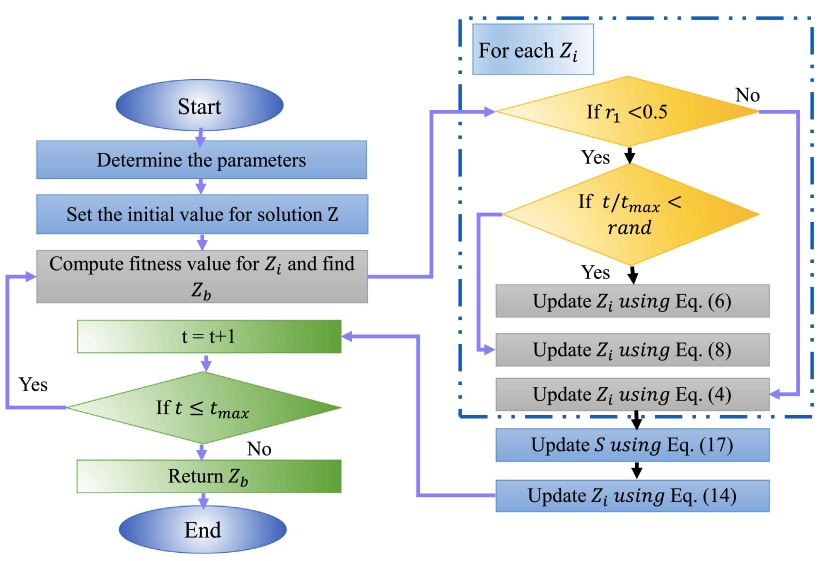
A Grunwald–Letnikov based Manta ray foraging optimizer for global optimization and image segmentation
This paper presents a modified version of Manta ray foraging optimizer (MRFO) algorithm to deal with global optimization and multilevel image segmentation problems. MRFO is a meta-heuristic technique that simulates the behaviors of manta rays to find the food. MRFO established its ability to find a suitable solution for a variant of optimization problems. However, by analyzing its behaviors during the optimization process, it is observed that its exploitation ability is less than exploration ability, which makes MRFO more sensitive to attractive to a local point. Therefore, we enhanced MRFO by
Control design approaches for parallel robot manipulators: A review
In this article, different control design approaches for parallel robot manipulators are presented with two distinguished classes of control strategies in the literature. These are the model-free control and the dynamic control strategy, which is mainly a model-based scheme, and is mostly the alternative when the control requirements are more stringent. The authors strongly believe that this paper will be helpful for researchers and engineers in the field of robotic systems. Copyright 2017 Inderscience Enterprises Ltd.
Further experimental evidence of the fractional-order energy equation in supercapacitors
Due to the dispersive porous nature of its material, carbon–carbon supercapacitors have a current–voltage relationship which is modeled by a fractional-order differential equation of the form i(t)=Cα[Formula presented] where α≤1 is a dispersion coefficient and Cα is a pseudo-capacitance not measurable in Farads. Hence, the energy stored in a capacitor, known to equal CV2/2 where C is the capacitance in Farad and V is the voltage applied, does not apply to a supercapacitor. In a recent work (Allagui et al., 2016), a fractional-order energy equation that enables the quantification of the energy
Fuzzy firefly clustering for tumour and cancer analysis
Swarm intelligence represents a meta-heuristic approach to solve a wide variety of problems. Searching for similar patterns of genes is becoming very essential to predict the expression of genes under various conditions. Firefly clustering inspired by the behaviour of fireflies helps in grouping genes that behave alike. Contrasting hard clustering methodology, fuzzy clustering assigns membership values for every gene and predicts the possibility of belonging to every cluster. To distinguish highly expressed and suppressed genes, the research in this paper proposes an efficient fuzzy-firefly
Fractional-order mathematical model for Chronic Myeloid Leukaemia
This paper is dedicated to develop a fractional order model of the rate of change of cancerous blood cells in Chronic Myeloid Leukaemia using fractional-order differential equations as well as tackling the factors that affect this rate and compare between them. The simulated cases (using MATLAB) prove that the proposed model is doable in terms of the variables positions in the equations and its effect on the overall population. Also, the effect of the Pactional order is investigated through three parameters sets and it has shown strong influence on the dynamic response. © 2017 IEEE.

Noise-estimation-based anisotropic diffusion approach for retinal blood vessel segmentation
Recently, numerous research works in retinal-structure analysis have been performed to analyze retinal images for diagnosing and preventing ocular diseases such as diabetic retinopathy, which is the first most common causes of vision loss in the world. In this paper, an algorithm for vessel detection in fundus images is employed. First, a denoising process using the noise-estimation-based anisotropic diffusion technique is applied to restore connected vessel lines in a retinal image and eliminate noisy lines. Next, a multi-scale line-tracking algorithm is implemented to detect all the blood
Analytical solution for fractional derivative gas-flow equation in porous media
In this paper, we introduce an analytical solution of the fractional derivative gas transport equation using the power-series technique. We present a new universal transform, namely, generalized Boltzmann change of variable which depends on the fractional order, time and space. This universal transform is employed to transfer the partial differential equation into an ordinary differential equation. Moreover, the convergence of the solution has been investigated and found that solutions are unconditionally converged. Results are introduced and discussed for the universal variable and other
Pagination
- Previous page ‹‹
- Page 29
- Next page ››
