Reduced-complexity SFBC-OFDM for vehicular channels with high mobility
Space frequency block coding with orthogonal frequency division multiplexing (SFBC-OFDM) suffers from the effect of inter-carrier interference (ICI) in doubly-selective communication channels. In this paper, a scheme is proposed in which windowing is applied to the received signal to reduce the effect of ICI to a limited number of neighboring sub-carriers. The sub-carriers holding the SFBC components of each codeword are separated by a number of sub-carriers larger than the ICI range, and hence, they do not interfere with each other. In order to preserve the structure of the SFBC, the
Towards optimal power control for delay-constrained cognitive radio networks
In this paper we study the problem of optimal power control for a Z-interference channel abstracting an underlay cognitive radio network where the secondary user has delay constraints. More specifically, we minimize the packet drop probability at the secondary user (equivalent to delay bound violation probability) subject to quality of service (QoS) constraints at the primary and secondary users, among other constraints. Towards, this objective, we develop a mathematical framework using Markov chains and formulate a constrained optimization problem. First, we assess the complexity of the
Towards optimal resource allocation in caching at relay networks
We investigate the performance of caching in relay networks where an intermediate relay station (RS) caches content for future demand by end users. With uncertain user demand over multiple data items and dynamically changing wireless links, we characterize the optimal transmission time for serving data items, cached data portion allocation of relay station and optimal service portion, which represents a part from the cached portion, to minimize the total average transmission energy. We argue that under several settings fully caching the higher popular items is the optimal caching policy which
Towards Mobility-Aware Proactive Caching for Vehicular Ad hoc Networks
Harnessing information about the user mobility pattern and daily demand can enhance the network capability to improve the quality of experience (QoE) at Vehicular Ad- Hoc Networks (VANETs). Proactive caching, as one of the key features offered by 5G networks, has lately received much interest. However, more research is still needed to convey large-sized multimedia content including video, audio and pictures to the high speed moving vehicles. In this paper, we study the gains achieved by proactive caching in Roadside Units (RSUs) where we take into consideration the effect of the vehicle
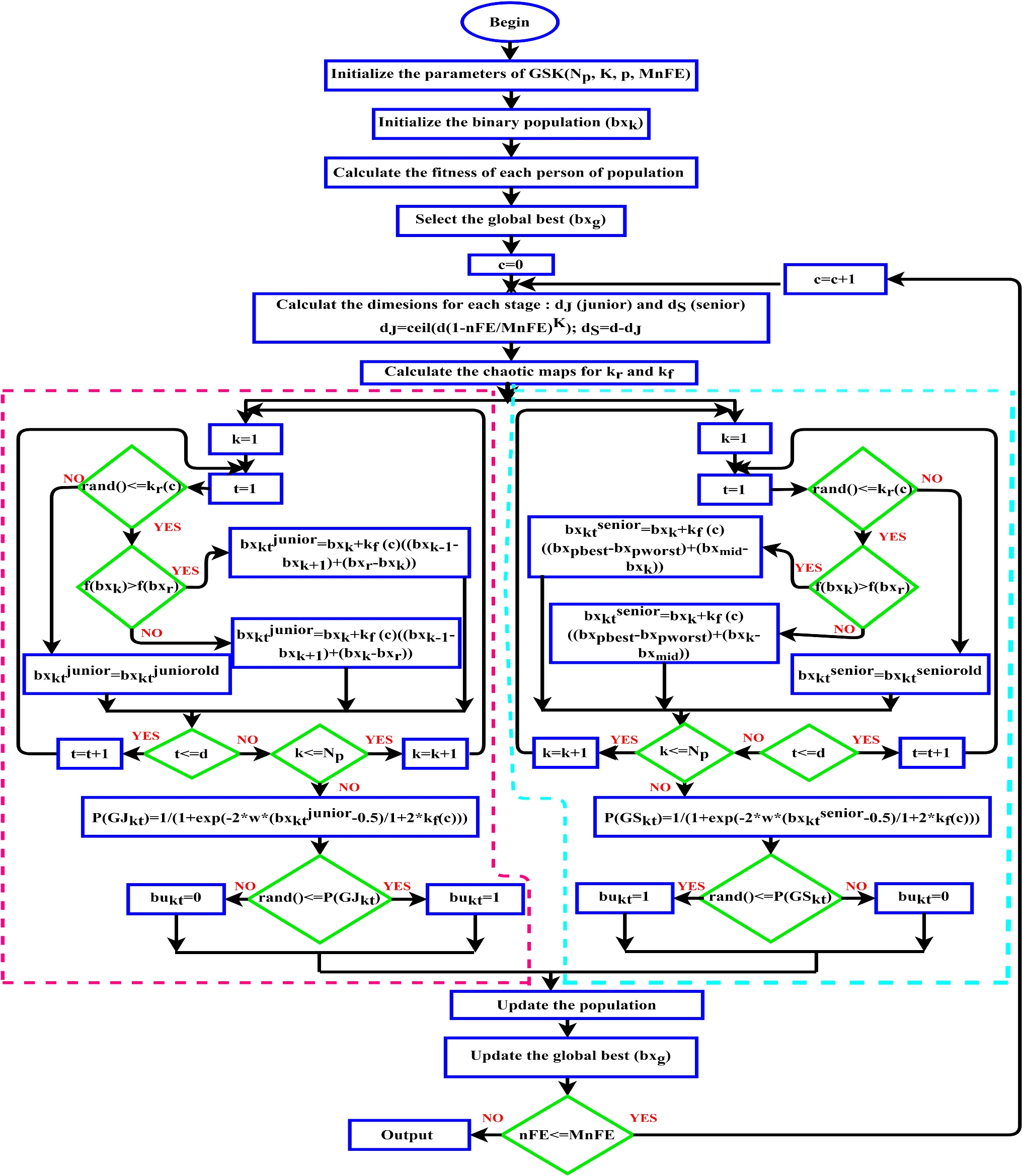
Chaotic gaining sharing knowledge-based optimization algorithm: an improved metaheuristic algorithm for feature selection
The gaining sharing knowledge based optimization algorithm (GSK) is recently developed metaheuristic algorithm, which is based on how humans acquire and share knowledge during their life-time. This paper investigates a modified version of the GSK algorithm to find the best feature subsets. Firstly, it represents a binary variant of GSK algorithm by employing a probability estimation operator (Bi-GSK) on the two main pillars of GSK algorithm. And then, the chaotic maps are used to enhance the performance of the proposed algorithm. Ten different types of chaotic maps are considered to adapt the
AROMA: Automatic generation of radio maps for localization systems
Current methods for building radio maps for wireless localization systems require a tedious, manual and error-prone calibration of the area of interest. Each time the layout of the environment is changed or different hardware is used, the whole process of location fingerprinting and constructing the radio map has to be repeated. The process gets more complicated in the case of localizing multiple entities in a device-free scenario, since the radio map needs to take all possible combinations of the location of the entities into account. In this demo, we present a novel system (AROMA) that is
Transmission power adaptation for cognitive radios
In cognitive radio (CR) networks, determining the optimal transmission power for the secondary users (SU) is crucial to achieving the goal of maximizing the secondary throughput while protecting the primary users (PU) from service disruption and interference. In this paper, we propose an adaptive transmission power scheme for cognitive terminals opportunistically accessing a primary channel. The PU operates over the channel in an unslotted manner switching activity at random times. The secondary transmitter (STx) adapts its transmission power according to its belief regarding the PU's state of
Hierarchical proactive caching for vehicular ad hoc networks
Recently, emerging vehicular applications are increasing the demand of vehicles which form significant burdens on network backhaul and represents a cause to the quality of experience (QoE) decay of the vehicular users. Proactive caching is a promising technique to mitigate the load on core networks by caching some of the expected data items. This work proposes a hierarchical proactive caching scheme which jointly considers caching in vehicles and roadside units (RSUs). Minimization of the vehicle communication latency is the main objective of our study. The optimization problem is formulated
Towards evolving sensor actor networks
Sensor Actor NETworks (SANET) represent a major component of ubiquitous service environments promising interesting solutions to a wide range of problems. Despite the obvious increase in the research activities proposing architectures and protocols for SANETs, we are still no where near the production of industrial-grade SANET software that can be relied upon for mission critical applications. The cost of programming, deploying and maintaining SANET environments is still highly prohibitive due to the lack of industrial tools capable of realizing adaptive SANET software in a cost effective way

Multi-reader RFID tag identification using bit tracking (MRTI-BT)
In this paper we study the problem of tag identification in multi-reader RFID systems. In particular, we propose a novel solution to the reader-to-reader collisions and tag collisions in multi-reader systems, using the concept of bit tracking [1]. Towards this objective, we propose the multi-reader RFID tag identification using bit tracking (MRTI-BT) algorithm which allows concurrent tag identification, by neighboring RFID readers, as opposed to time-consuming scheduling. First, MRTI-BT identifies tags exclusive to different RFIDs, concurrently. Second, the concept of bit tracking and the
Pagination
- Previous page ‹‹
- Page 18
- Next page ››
