Breadcrumb
Optimum distribution of protective materials for COVID−19 with a discrete binary gaining-sharing knowledge-based optimization algorithm
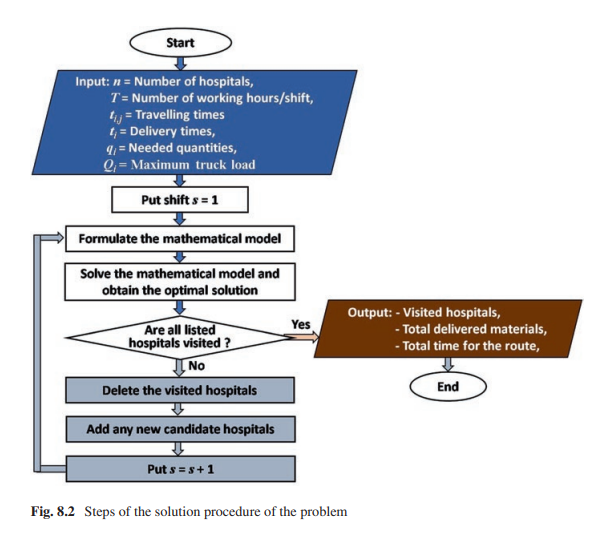
Many application problems are formulated as nonlinear binary programming models which are hard to be solved using exact algorithms especially in large dimensions. One of these practical applications is to optimally distribute protective materials for the newly emerged COVID-19. It is defined for a decision-maker who wants to choose a subset of candidate hospitals comprising the maximization of the distributed quantities of protective materials to a set of chosen hospitals within a specific time shift. A nonlinear binary mathematical programming model for the problem is introduced with a real application case study; the case study is solved using a novel discrete binary gaining-sharing knowledge-based optimization algorithm (DBGSK). The solution algorithm proposes a novel binary adaptation of a recently developed gaining-sharing knowledge-based optimization algorithm (GSK) to solve binary optimization problems. GSK algorithm is based on the concept of how humans acquire and share knowledge through their life span. Discrete binary version of GSK named novel binary gaining-sharing knowledge-based optimization algorithm (DBGSK) depends mainly on two binary stages: binary junior gaining-sharing stage and binary senior gaining-sharing stage with knowledge factor 1. These two stages enable DBGSK for exploring and exploitation of the search space efficiently and effectively to solve problems in binary space. © Springer Nature Switzerland AG 2021.