Fractional-order inverting and non-inverting filters based on CFOA
This paper introduces a study to generalize the design of a continuous time filters into the fractional order domain. The study involves inverting and non-inverting filters based on CFOA where three responses are extracted which are high-pass, band-pass and low-pass responses. The proposed study introduces the generalized formulas for the transfer function of each response with different fractional orders. The fractional-order filters enhance the design flexibility and controllability due to the extra degree of freedom provided by the fractional order parameters. The general fundamentals of
Fractional Order Oscillator Design Based on Two-Port Network
In this paper, a general analysis of the generation for all possible fractional order oscillators based on two-port network is presented. Three different two-port network classifications are used with three external single impedances, where two are fractional order capacitors and a resistor. Three possible impedance combinations for each classification are investigated, which give nine possible oscillators. The characteristic equation, oscillation frequency and condition for each presented topology are derived in terms of the transmission matrix elements and the fractional order parameters α
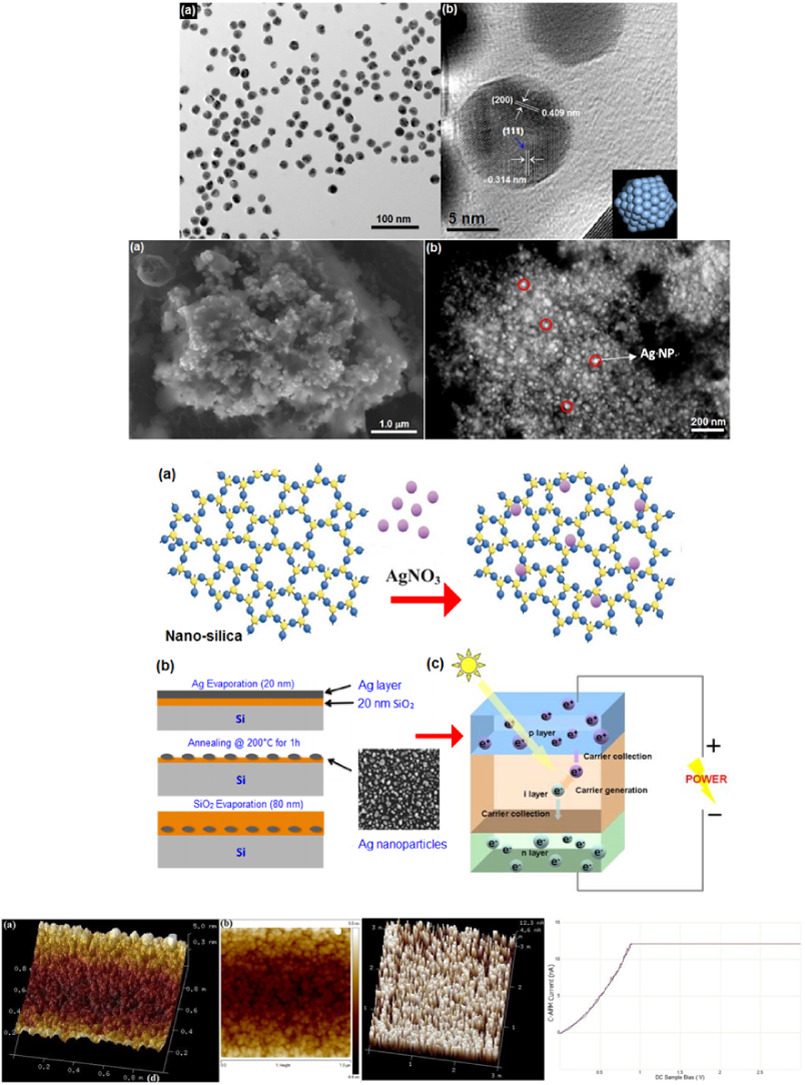
Aggrandize efficiency of ultra-thin silicon solar cell via topical clustering of silver nanoparticles
A highly efficient photovoltaic nanocomposite device is demonstrated by fabrication of structural clusters of silver nanoparticles (Ag NPs) on silicon solar cells via a boil deposition method. The efficiency of silicon solar cell was augmented by coating Ag NPs ultra-thin-film deposition on silicon solar cell. Chemically synthesized silver NP's, their consumption on a silicon thin layer and the operation of photovoltaic nanocomposite device were characterized by using several electron probe microscopic pectroscopic and spectrometric techniques viz. x-ray diffraction (XRD), scanning electron
FPGA realization of Caputo and Grünwald-Letnikov operators
This paper proposes a hardware platform implementation on FPGA for two fractional-order derivative operators. The Grünwald-Letnikov and Caputo definitions are realized for different fractional orders. The realization is based on non-uniform segmentation algorithm with a variable lookup table. A generic implementation for Grünwald-Letnikov is proposed and a 32 bit Fixed Point Booth multiplier radix-4 is used for Caputo implementation. Carry look-ahead adder, multi-operand adder and booth multiplier are used to improve the performance and other techniques for area and delay minimization have
Fractional order four-phase oscillator based on double integrator topology
This paper presents a generalization of Soliman's four-phase oscillator into the fractional-order domain. The extra degrees of freedom provided by the fractional-order parameters α and β add more flexibility to the design of the circuit. The design procedure and equations of the proposed oscillator are presented and verified using Matlab and PSPICE. Also, the stability analysis for fractional order systems is studied for different cases of α and β. © 2017 IEEE.

Biological inspired optimization algorithms for cole-impedance parameters identification
This paper introduces new meta-heuristic optimization algorithms for extracting the parameters of the Cole-impedance model. It is one of the most important models providing best fitting with the measured data. The proposed algorithms inspired by nature are known as Flower Pollination Algorithm (FPA) and Moth-Flame Optimizer (MFO). The algorithms are tested over sets of both simulated and experimental data. The results are compared with other fitting algorithms such as the Non-linear least square (NLS) and Bacterial Foraging Optimization (BFO). The comparison showed a better fit in the sum of
FPGA Implementation of X- and Heart-shapes Controllable Multi-Scroll Attractors
This paper proposes new multi-scrolls chaotic systems which is called the X-shape. The purpose is to have more complex systems and flexible ranges of the chaotic behavior. The proposed X-shape is a combination between V-shape and Λ-shape. This paper also represents the Heart-shape which considered a special case of the X-shape. The system complexity has been measured by MLE and compared with V-shape system. It shows lager MLE on the side of X-shape. In addition, the effect of changing system parameters has been discussed and compared with V-shape. Finally, a fully hardware implantation on FPGA
Comparison between three approximation methods on oscillator circuits
The promising capabilities of fractional-order devices challenge researchers to find a way to build it physically. Approximating the Laplacian operator sα can pave the way to emulate the fractional-order devices till its off-the-shelf appearance. This paper introduces three approximations of the Laplacian operator sα: Oustaloup, Matsuda, and Valsa by comparing their behaviors through two types of oscillator circuits. The first two are well-established approximations and the latter is proposed for the first time by converting its model network to an integer polynomial approximation of the
Fractional-Order Relaxation Oscillators Based on Op-Amp and OTRA
This paper introduces closed formulas of two topologies of fractional-order relaxation oscillators. One of these topologies is based on Operational Amplifier (Op-Amp) and the other one depends on Operational Operational Trans-Resistance Amplifier (OTRA). Special cases for each topology are also provided. The advantage of these designs comes from the added extra degree of freedom presented by the fractional-order α. Matsuda's approximation of sα is used to implement fractional-order capacitors. Also, experimental work is included to verify the theoretical results. © 2018 IEEE.
Fractional-order Nonminimum-phase Filter Design
This paper introduces the design procedure of the fractional-order Soliman Nonminimum-phase filter. Theoretical analysis has been carried out providing the critical frequencies of the filter. The effect of fractional-order parameter \alpha on the filter response has been investigated. Additionally, two different approximation techniques (Oustaloup and Matsuda) have been employed to realize the filter. A comparison is held between the exact and approximated solutions. Theoretical analysis is verified through circuit simulations and experimental work. © 2019 IEEE.
Pagination
- Previous page ‹‹
- Page 8
- Next page ››
