Breadcrumb
Stochastic modeling of mushroom—waveguide photodetectors
Waveguide photodetectors (WGPDs) are one of the promising candidates to solve the tradeoff between the quantum efficiency and the transit time in the surface illuminated photodiodes where the lightwave is incident laterally perpendicular to the direction of the flow of generated carriers, enhancing both high speed and quantum efficiency. In Mushroom-WGPDs, the performance degradation due its parasitic capacitance and the load resistance is overcome due to the mesa mushroom structure. Inaccuracies in the dimensions of’Mushroom-WGPDs due to the fabrication affect its functionality and its
Stochastic modeling of 2D photonic crystals
Due to the fabrication processes, inaccurate manufacturing of the photonic crystals (PCs) might occur which affect their performance. In this paper, we examine the effects of tolerance variations of the radii of the rods and the permittivity of the material of the two-dimensional PCs on their performance. The presented stochastic analysis relies on plane wave expansion method and Mote Carlo simulations. We focus on two structures, namely Si-Rods PCs and Air-Holes PCs. Numerical results show—for both structures—that uncertainties in the dimensions of the PCs have higher impact on its photonic
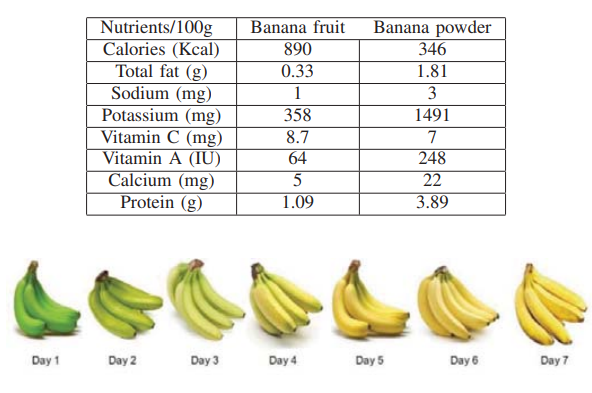
Banana ripening and corresponding variations in bio-impedance and glucose levels
This paper studies banana fruit ripping using the Cole-impedance model fitted over the measured bio-impedance data by monitoring the changes in the model parameters during the different ripping stages. A set of twenty bananas are tested for 84 hours, and impedance measurements are done every 12 hours using an SP150 electrochemical station. The changes in model parameters are related to the physical changes in the fruit as well as with the glucose concentration, which increases with time. © 2019 IEEE.
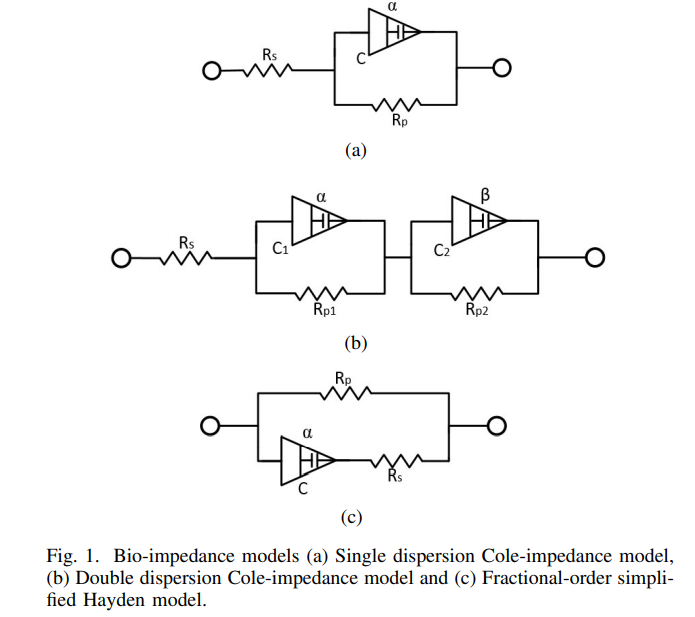
Do the Bio-impedance Models Exhibit Pinched Hysteresis?
Recently, pinched hysteresis has been found in the electrical modelling of regular plant tissues. Usually, the biological tissues are characterized in the frequency domain using bio-impedance analyzers without investigating the time domain, which would show the pinched hysteresis. In this paper, the current-voltage analysis of some of the widely known electrical bio-impedance models is studied. The investigated models are the single dispersion Cole-impedance model, the double dispersion Cole-impedance model and the fractional-order simplified Hayden model to prove that these models can not
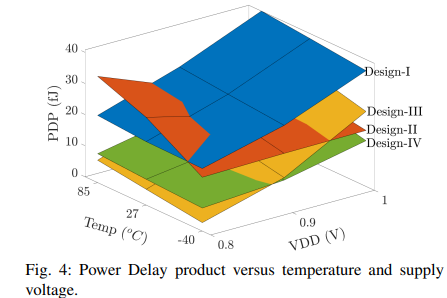
Comparative Study of CNTFET Implementations of 1-trit Multiplier
Ternary logic has become a promising alternative to traditional binary logic due to low power consumption and reduced circuits such as interconnects and chip areas. The efficiency of the multiplier circuit can be much better using a ternary logic system. Carbon nanotube field-effect transistor (CNTFET) is a promising technology as it achieves more advantages than MOSFET due to its low off-current features such as low power and high performance. This paper presents a comparative study of four implementations of a 1-trit multiplier based on CNTFET technology. The comparison is performed in terms
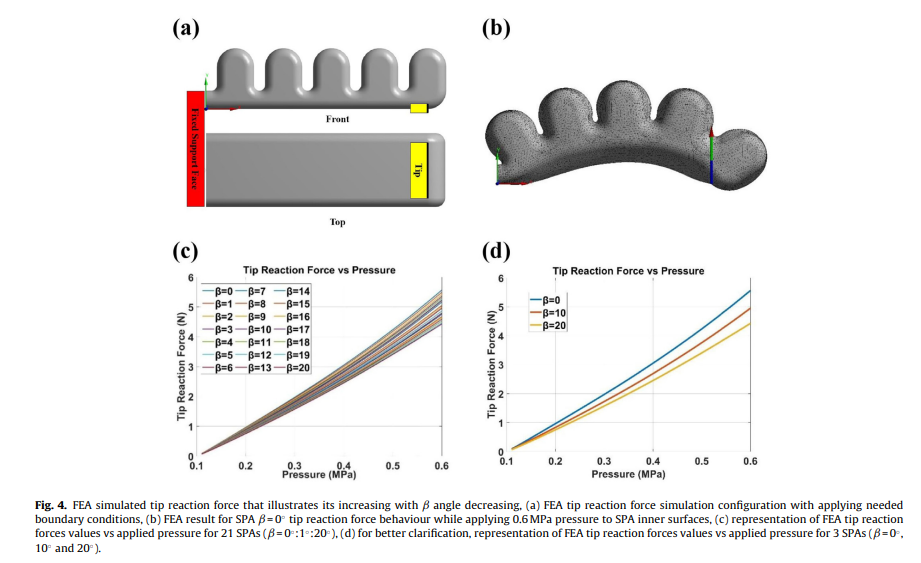
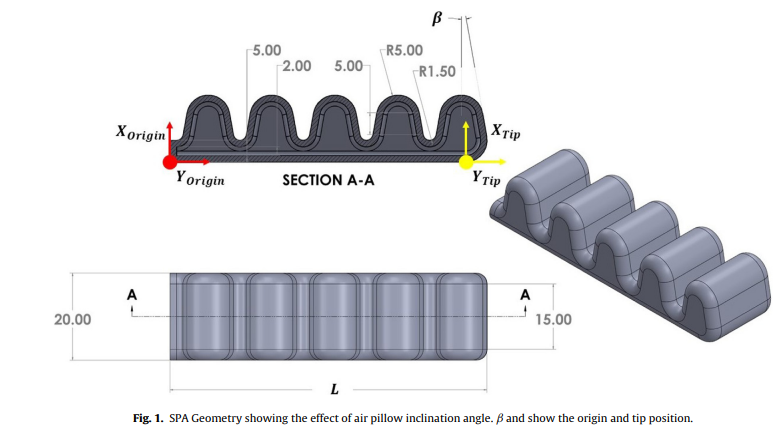
Design and implementation of variable inclined air pillow soft pneumatic actuator suitable for bioimpedance applications
The technological revolution has caused the modernization of human–machine relationship changing our approach in problem solving our society issues and deviated the science of robotic all together. An example for one of the most important pawn in this revolution is soft robotics, the soft robots are robots that are made of deformable materials that provide an alternative approach to rigid robots. The soft pneumatic actuator (SPA) is one of the most widely used and studied form of this type of robotics. In this study, a new geometrical parameter of the SPAs is introduced by studying the effect
Theoretical and experimental investigation study of data driven work envelope modelling for 3D printed soft pneumatic actuators
In the last decade, soft robotics is considered one of the most widely researched fields in robotics, as it has many advantages and more versatile use than rigid robotics. Soft robots are flexible, which enable them to metaphorically complex designs, enabling them to imitate the movement of living things. In this article, the use of regression models with finite element analysis (FEA) data is compared with neural network (NN) models trained on visual feedback data. The effect of the soft pneumatic actuator (SPA) air pillow inclination angle (β) under positive and vacuum pressure on the
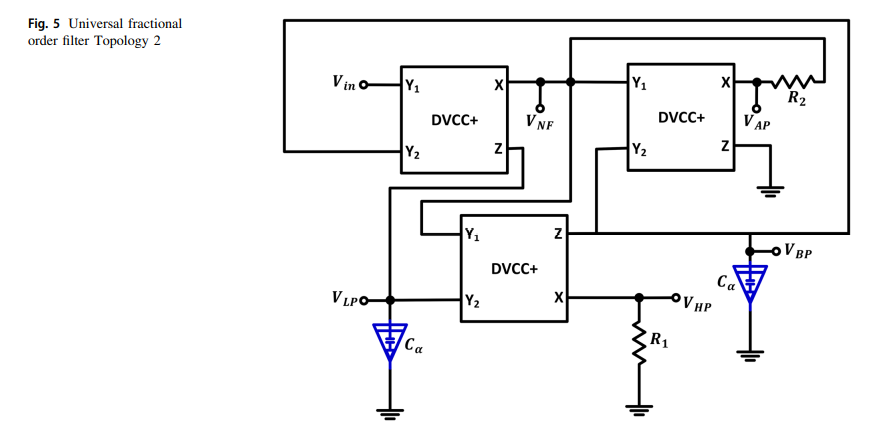
α -order universal filter realization based on single input multi-output differential voltage current conveyor
Two voltage-mode topologies single input multi-output universal fractional filters with high input impedance are proposed. The proposed analog filters consist of three DVCC+ blocks, two grounded capacitors and two resistors targeting the minimum passive elements. The proposed topologies provide a realization for all standard fractional filter functions (HP, LP, BP, AP and notch filter). The effect of Fractional order on filter responses in the range of α from 0.7 to 1.2 was studied. Fractional order has been investigated for different filter responses in terms of cutoff, gain, phase and noise
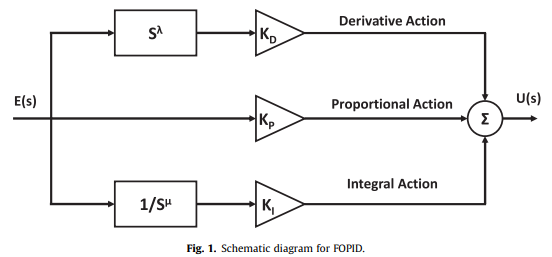
Optimal fractional-order PI with DC-DC converter and PV system
This paper presents a design and analysis for the PV system with a DC-DC boost converter controlled by the Fractional Order PI controller (FOPI). The study includes obtaining the optimal parameters for the PV model and the operating parameters for the FOPI controller. The first part's objective function is to search a five-parameter model based on the data-sheet given by commercial PV modules for a single-diode (SD) model. In the second part of the study, a detailed comparison is executed versus P, PI, PID, and FOPI controllers showing the effect of implementing Fractional order controllers on
Power tracking controller design for photo-voltaic systems based on particle swarm optimization technique
Solar energy turns into a promising supply of electricity, so structures of Photo-voltaic (PV) regularly use a maximum power point tracking (MPPT) way to deliver the highest probable power to the load continuously. This paper presents the methodology of PI controller tuning of PV employing Particle Swarm Optimization (PSO). The aim is to obtain the maximum power and maintain its value using the PI controller. It is employed to trace this highest power point value. © 2019 IEEE.
Pagination
- Previous page ‹‹
- Page 49
- Next page ››
