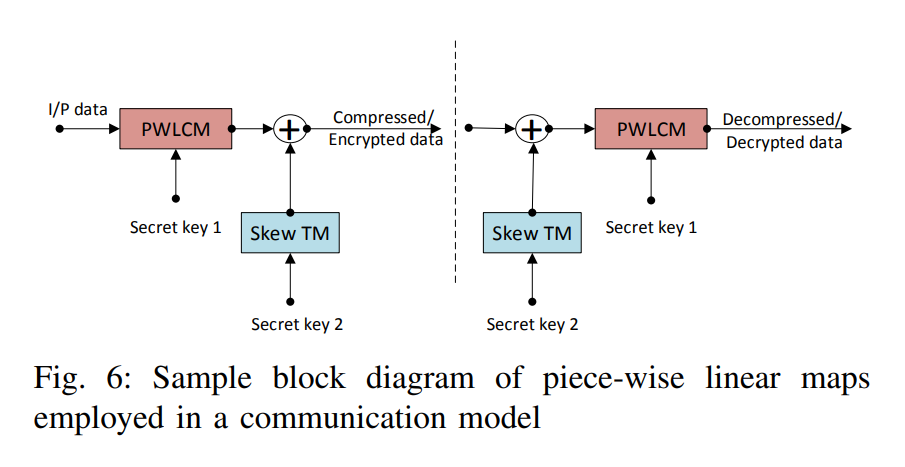
Double-sided bifurcations in tent maps: Analysis and applications
The tent map is a piece-wise linear one-dimensional discrete map which could be implemented easily. In this paper, a signed system parameter is allowed leading to the appearance of bidirectional bifurcations. A set of proposed tent maps with different sign variations and a signed parameter are investigated where the conventional map is a special case. The proposed maps exhibit period doubling as a route to chaos with wider and alternating sign output ranges that could fit multiple applications. Based on the maximum achievable output range corresponding to maximum chaotic behavior, the

Analysis of a rectifier circuit realized with a fractional-order capacitor
An analysis of a traditional rectifier circuit when a fractional-order capacitor with order 0 < α < 1 replaces the integer-order smoothing capacitor (α = 1) is presented. Exploring the change in discharging behaviour that results from this replacement and the impacts on ripple voltage, nominal DC voltage, current, and power expressions used to describe the performance of this class of circuits. Further, the assumptions made for the analysis of the traditional circuit are explored from the fractional perspective to determine if they are still valid. © 2016 IEEE.
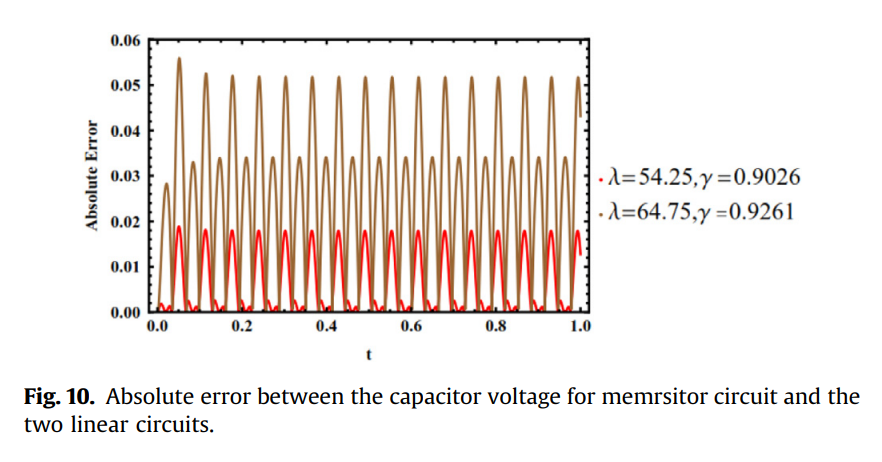
An optimal linear system approximation of nonlinear fractional-order memristor-capacitor charging circuit
The analysis of nonlinear fractional-order circuits is a challenging problem. This is due to the lack of nonlinear circuit theorems and designs particularly in the presence of memristive elements. The response of a series connection of a simple resistor with fractional order capacitor and its analytical formulation in both charging and discharging phases is considered. The numerical simulation of fractional order HP memristor in series with a fractional order capacitor is also discussed. It is a demonstration of a simple nonlinear fractional-order memristive circuit in both charging and
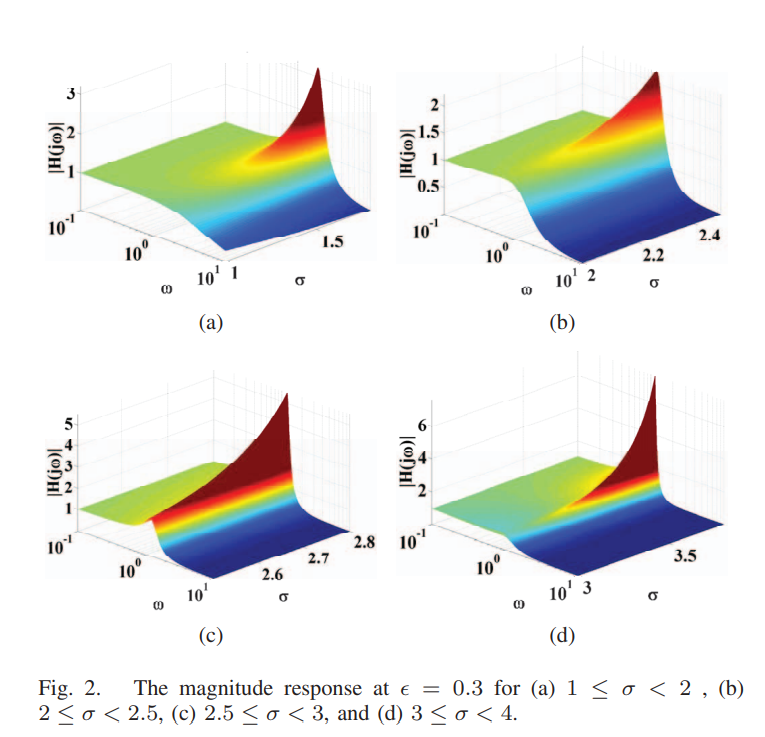
Low pass filter design based on fractional power chebyshev polynomial
This paper introduces the design procedure for the low pass filter based on Chebyschev polynomials of fractional power of any order. The filter order is considered in intervals of width two. Only the first two intervals are considered along with their pole locus produced by varying the filter order and the magnitude response. A general formula for constructing the filter from its s-plane poles is suggested. Numerical analysis and circuit simulations using MATLAB and Advanced Design System (ADS) based on the proposed design procedure are presented. Good matching between the circuit simulation
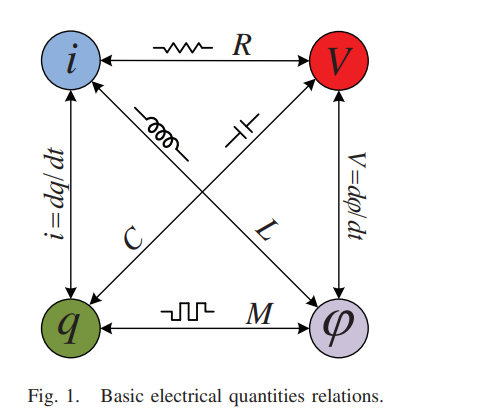
Review of the missing mechanical element: Memdamper
In this paper, the analogy between electrical and mechanical quantities is reviewed. Based on this analogy, there is a missing link between displacement and momentum. This missing link corresponds to the link between the charge and flux which represents the memristor. This link is still missing between the mechanical quantities. In this work, we shed the light on this missing mechanical element. We introduce the mathematical relation which links displacement and momentum. Two main types of missing relations are discussed. © 2015 IEEE.
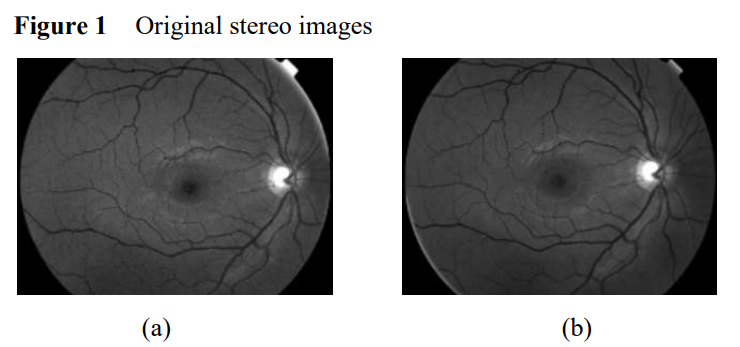
3D surface reconstruction of retinal vascular structures
We propose in this paper, a three-dimensional surface reconstruction of a retinal vascular network from a pair of 2D retinal images. Our approach attempts to address the above challenges by incorporating an epipolar geometry estimation and adaptive surface modelling in a 3D reconstruction, using three steps: segmentation, 3D skeleton reconstruction and 3D surface modelling of vascular structures. The intrinsic calibration matrices are found via the solution of simplified Kruppa equations. A simple essential matrix based on a self-calibration method has been used for the 'fundus camera-eye'
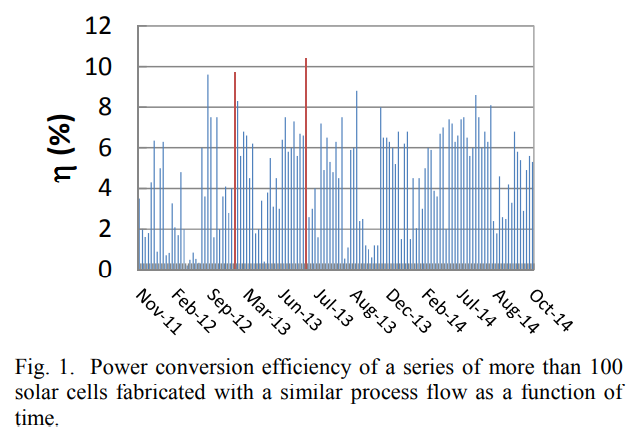
Process variability in Cu2ZnSnSe4 solar cell devices: Electrical and structural investigations
We have fabricated 9.7% efficient Cu2ZnSnSe4/CdS/ZnO solar cells by H2Se selenization of sequentially sputtered metal layers. Despite the good efficiency obtained, process control appears to be difficult. In the present contribution we compare the electrical and physical properties of two devices with nominal same fabrication procedure, but 1% and 9.7% power conversion efficiency respectively. We identify the problem of the lower performing device to be the segregation of ZnSe phases at the backside of the sample. This ZnSe seems to be the reason for the strong bias dependent photocurrent
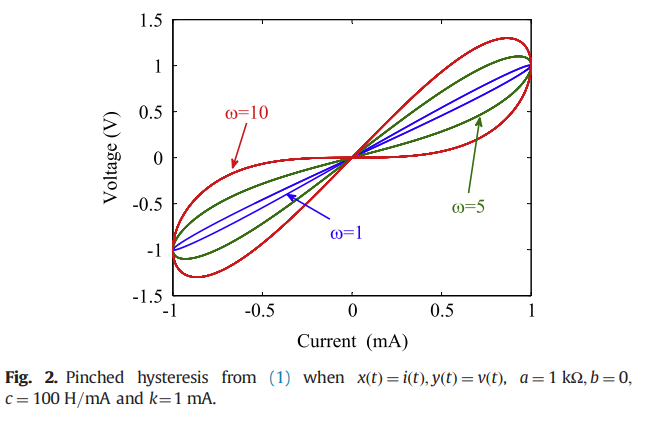
Pinched hysteresis with inverse-memristor frequency characteristics in some nonlinear circuit elements
Abstract Pinched hysteresis is considered to be a signature of the existence of memristance. However, here we report on a model that exhibits pinched hysteresis yet it may represent a nonlinear inductor or a nonlinear capacitor (both with quadratic nonlinearity) or a derivative-controlled nonlinear resistor/transconductor. Further, the lobe area of the pinched hysteresis loop in these devices has inverse-memristor characteristics; i.e. it is observed to widen rather than decline with increased operating frequency. Experimental results are provided to validate the model. © 2015 Elsevier Ltd.
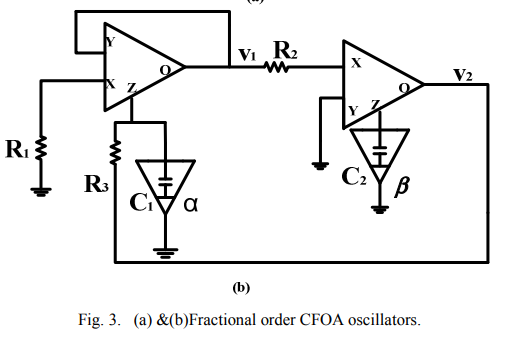
Current feedback operational amplifier (CFOA) based fractional order oscillators
This paper presents a study of fractional order oscillators based on current feedback operational amplifiers (CFOA). Two general cases have been discussed for the oscillation frequency and condition with the use of two fractional order elements of different orders. Design procedure for the two general cases is illustrated with numerical discussions. Circuit simulations for some special cases are presented to validate the theoretical findings. The simulations have been done using Ad844 commercial CFOA model © 2014 IEEE.
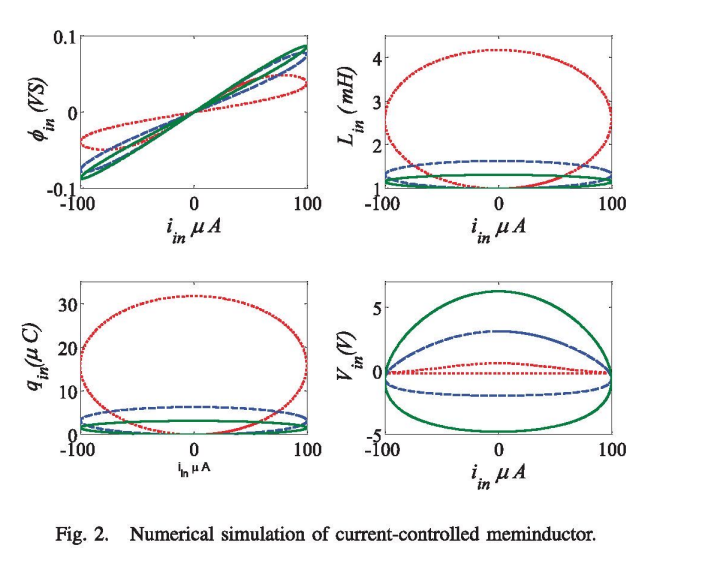
Memristor-less current- and voltage-controlled meminductor emulators
This paper introduces two mathematical models of meminductor based on a simple symmetrical double-loop equation with their generic formulas and analysis. Moreover, new circuits based on CCII are developed for emulating the behavior of the current-controlled and voltage-controlled models. The proposed circuits are realized without using a memristor unlike the previous emulators. Finally, the proposed emulators are verified using PSPICE simulations. © 2014 IEEE.
Pagination
- Previous page ‹‹
- Page 40
- Next page ››
