Breadcrumb
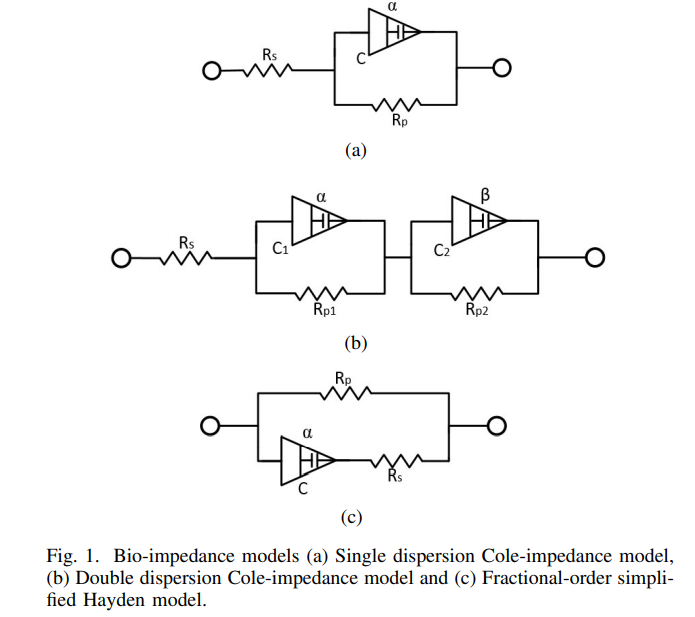
Do the Bio-impedance Models Exhibit Pinched Hysteresis?
Recently, pinched hysteresis has been found in the electrical modelling of regular plant tissues. Usually, the biological tissues are characterized in the frequency domain using bio-impedance analyzers without investigating the time domain, which would show the pinched hysteresis. In this paper, the current-voltage analysis of some of the widely known electrical bio-impedance models is studied. The investigated models are the single dispersion Cole-impedance model, the double dispersion Cole-impedance model and the fractional-order simplified Hayden model to prove that these models can not
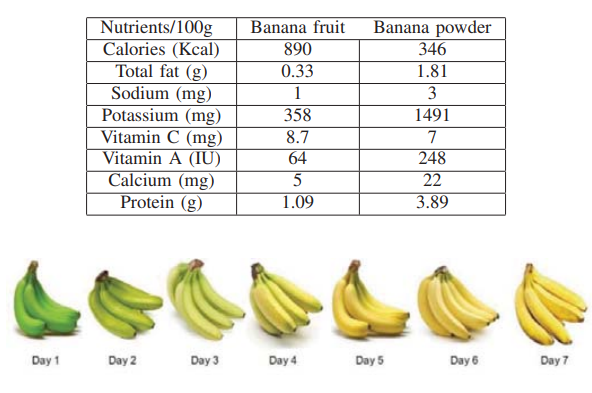
Banana ripening and corresponding variations in bio-impedance and glucose levels
This paper studies banana fruit ripping using the Cole-impedance model fitted over the measured bio-impedance data by monitoring the changes in the model parameters during the different ripping stages. A set of twenty bananas are tested for 84 hours, and impedance measurements are done every 12 hours using an SP150 electrochemical station. The changes in model parameters are related to the physical changes in the fruit as well as with the glucose concentration, which increases with time. © 2019 IEEE.
Stochastic modeling of 2D photonic crystals
Due to the fabrication processes, inaccurate manufacturing of the photonic crystals (PCs) might occur which affect their performance. In this paper, we examine the effects of tolerance variations of the radii of the rods and the permittivity of the material of the two-dimensional PCs on their performance. The presented stochastic analysis relies on plane wave expansion method and Mote Carlo simulations. We focus on two structures, namely Si-Rods PCs and Air-Holes PCs. Numerical results show—for both structures—that uncertainties in the dimensions of the PCs have higher impact on its photonic
Stochastic modeling of mushroom—waveguide photodetectors
Waveguide photodetectors (WGPDs) are one of the promising candidates to solve the tradeoff between the quantum efficiency and the transit time in the surface illuminated photodiodes where the lightwave is incident laterally perpendicular to the direction of the flow of generated carriers, enhancing both high speed and quantum efficiency. In Mushroom-WGPDs, the performance degradation due its parasitic capacitance and the load resistance is overcome due to the mesa mushroom structure. Inaccuracies in the dimensions of’Mushroom-WGPDs due to the fabrication affect its functionality and its
Modeling of carrier mobility for semispherical quantum dot infrared photodetectors (QDIPs)
Carrier mobility for quantum dot infrared photodetectors is considered as one of the critical parameters to determine many important device’s performance parameters such as the electrical conductivity, drift velocity, dark current and photocurrent. In this paper a complete theoretical model of the carrier mobility for semispherical quantum dot structures is developed. This model is based on the solution of Boltzmann transport equation all over the device. A parametric study of the effects of the QD density and the dimensions of the QD on the carrier mobility is investigated. Finally, the
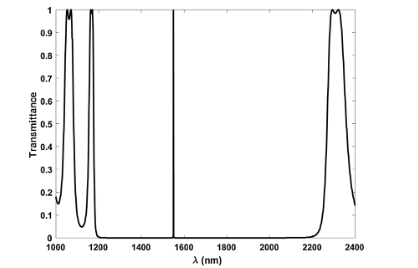
Stochastic analysis for one dimensional photonic crystals
Tolerance variations of the design parameters of the photonic crystals due to fabrication processes have a strong effect on the performance of the photonic crystals and their operating wavelengths. In this work, the uncertainties of the design parameters of one-dimensional photonic crystals (1D-PCs) and their impacts on the PCs optical properties and the operating performance are investigated. The effects of these uncertainties for different tolerances are studied for both defect-free PCs and PCs with a defect air layer. The probability distribution function and the standard deviations of the
Conical and cylindrical metallic nanoparticles design for plasmonic photovoltaics enhancement
Plasmonic Photovoltaics are considered as a promising candidate for enhancing the optical absorption by embedding metallic nanoparticles that confine the incident light in the cell. This results in thin-film PVs with improved efficiency. In this paper, the effects of embedding both conical and cylindrical metal nanoparticles in plasmonic PVs are investigated. The extinction cross sections for these designs are calculated. The improvement of the optical absorption of the solar cell due to these nanoparticles is proved and compared. Finally, the effects of the design parameters of these
Interfacial modification of perovskite solar cell using zno electron injection layer with pdms as antireflective coating
Recently, perovskite solar cells (PSCs) exhibits tremendous power conversion efficiency and has shown enhanced figures of merit being secured regarding cell stability. In this paper, perovskite solar cell with Zno electron injection layer is presented. The humidity degradation of the perovskite active layer and the efficiency of the cell is observed under several conditions. Using ZnO as a planner electron injection layer (EIL) instead of TiO2, the efficiency of the device significantly improved, showing low-resistance shunting pathways. Also, polydimethylsiloxane (PDMS) has been used as a
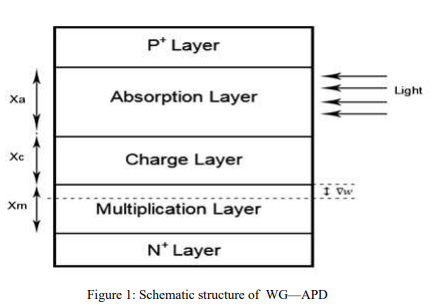
A Stochastic Modeling of the Gain in Waveguide Avalanche Photodetectors (WG-APDs)
Waveguide photodetectors are considered as a promising candidate for high speed photodetection where the tradeoff between the transit time bandwidth and the quantum efficiency is overcome as the incident optical signal and the photogenerated carriers move in perpendicular directions. In WG-Avalanche Photodetectors (WG-APDs), the avalanche multiplication gain enhances the photocurrent of the photodiodes. In these photodiodes, the inaccuracies in the ionizations coefficients of the photogenerated electrons and holes and in the dimensions of the multiplication layer affect the multiplication gain
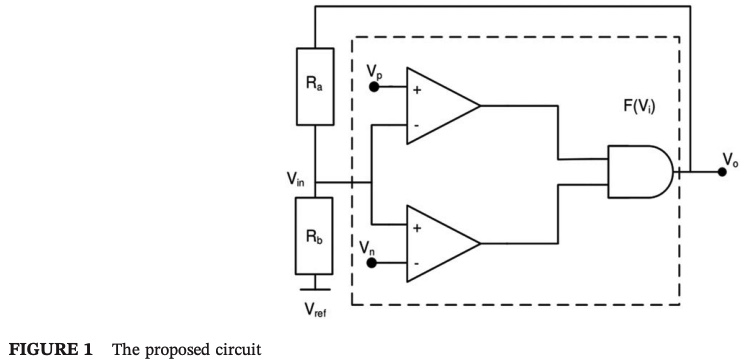
A generalized family of memristor-based voltage controlled relaxation oscillator
Recently, memristive oscillators are a significant topic in the nonlinear circuit theory where there is a possibility to build relaxation oscillators without existence of reactive elements. In this paper, a family of voltage-controlled memristor-based relaxation oscillator including two memristors is presented. The operation of two memristors-based voltage relaxation oscillator circuits is demonstrated theoretically with the mathematical analysis and with numerical simulations. The generalized expressions for the oscillation frequency and conditions are derived for different cases, where a
Pagination
- Previous page ‹‹
- Page 13
- Next page ››
