Breadcrumb
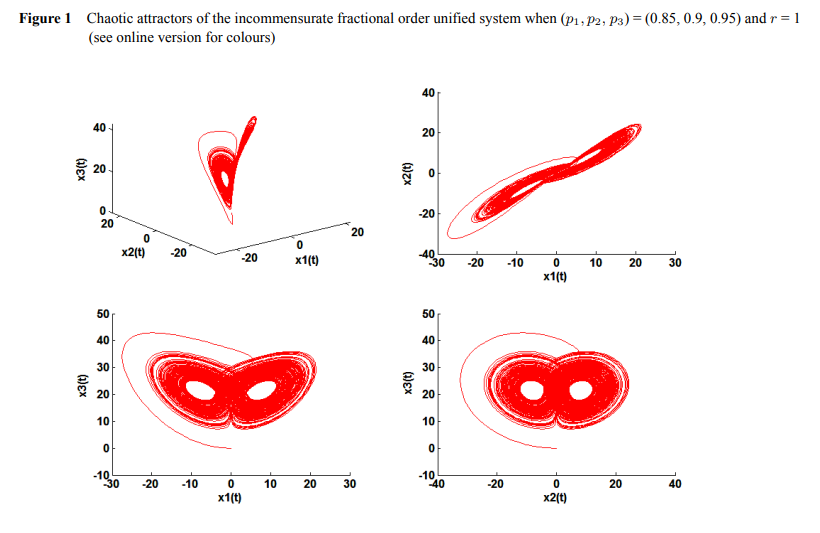
A new fractional hybrid chaos synchronisation
Over the last decades, synchronisation of chaotic systems has become an active research area and has been extensively and intensively studied due to the variety of important applications. Different types of chaos synchronisation have been presented, and many various methods and techniques for chaos synchronisation have been reported to investigate some types of chaos. In this paper, by combining full state hybrid projective synchronisation (FSHPS) and inverse full state hybrid projective synchronisation (IFSHPS), a new type of hybrid synchronisation between different dimensional incommensurate
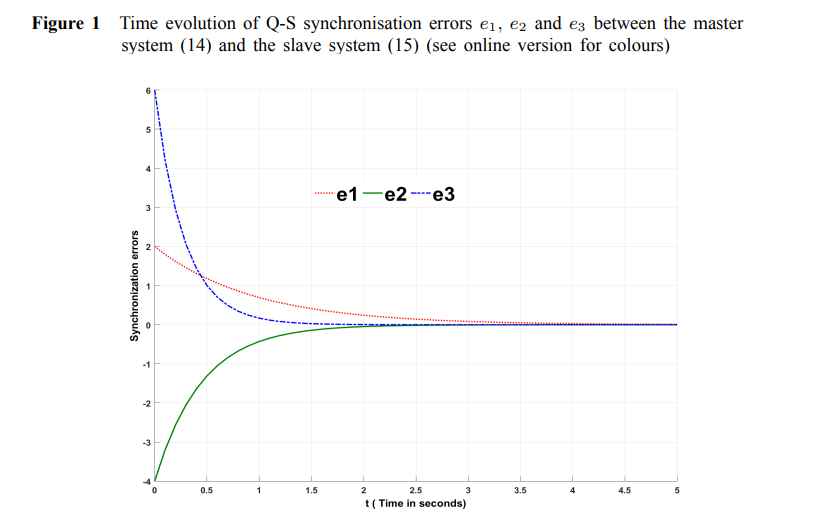
On a simple approach for Q-S synchronisation of chaotic dynamical systems in continuous-time
In this paper, the problem of Q-S synchronisation for arbitrary dimensional chaotic dynamical systems in continuous-time is investigated. Based on nonlinear control method, we would like to present a constructive scheme to study the Q-S synchronisation between n-dimensional master chaotic system and m-dimensional slave chaotic system in arbitrary dimension. The new derived synchronisation result is proved using Lyapunov stability theory. In order to verify the effectiveness of the proposed method, our approach is applied to some typical chaotic systems and numerical simulations are given to
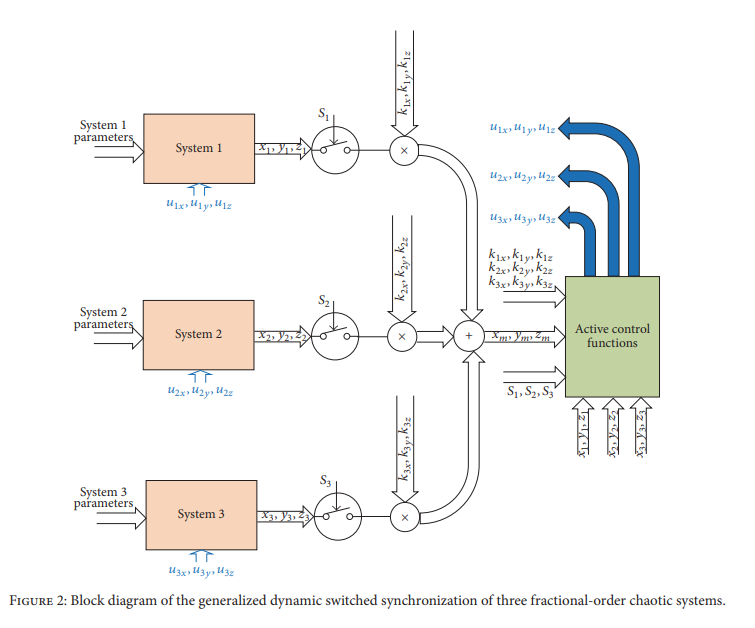
Generalized dynamic switched synchronization between combinations of fractional-order chaotic systems
This paper proposes a novel generalized switched synchronization scheme among n fractional-order chaotic systems with various operatingmodes. Digital dynamic switches and dynamic scaling factors are employed, which offermany new capabilities. Dynamic switches determine the role of each system as a master or a slave. A system can either have a fixed role throughout the simulation time (static switching) or switch its role one or more times (dynamic switching). Dynamic scaling factors are used for each state variable of the master system. Such scaling factors control whether the master is a
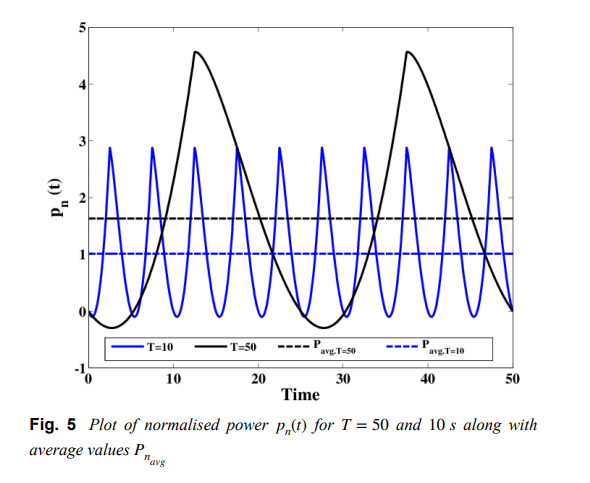
Low-voltage commercial super-capacitor response to periodic linear-with-time current excitation: A case study
The response of a commercial super-capacitor to an applied periodic current excitation in the form of a triangular waveform is investigated in this study. This waveform has a linear-with-time variation which enables linear charging and discharging of the device. A model consisting of a linear resistance Rs and a constant phase element is used to describe the super-capacitor impedance and expressions for the voltage across the device, the power, and stored energy are derived using concepts from fractional calculus. Experimental results are shown and an application of the study to super
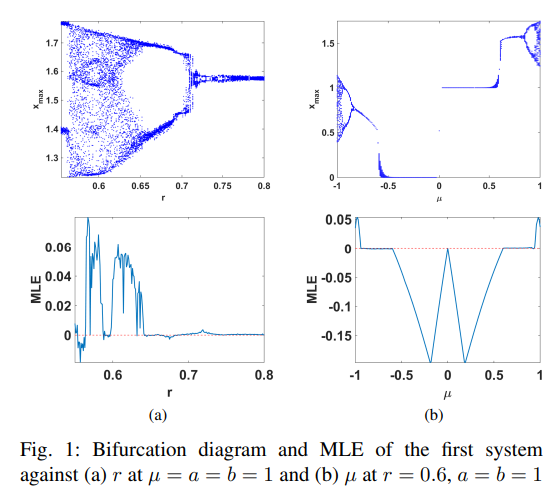
Chaotic systems based on jerk equation and discrete maps with scaling parameters
In the recent decades, applications of chaotic systems have flourished in various fields. Hence, there is an increasing demand on generalized, modified and novel chaotic systems. In this paper, we combine the general equation of jerk-based chaotic systems with simple scaled discrete chaotic maps. Numerical simulations of the properties of two systems, each with four control parameters, are presented. The parameters show interesting behaviors and dependencies among them. In addition, they exhibit controlling capabilities of the ranges of system responses, hence the size of the attractor diagram
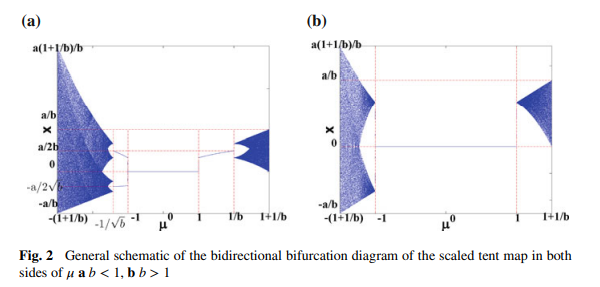
Chaos and bifurcation in controllable jerk-based self-excited attractors
In the recent decades, utilization of chaotic systems has flourished in various engineering applications. Hence, there is an increasing demand on generalized, modified and novel chaotic systems. This chapter combines the general equation of jerk-based chaotic systems with simple scaled discrete chaotic maps. Two continuous chaotic systems based on jerk-equation and discrete maps with scaling parameters are presented. The first system employs the scaled tent map, while the other employs the scaled logistic map. The effects of different parameters on the type of the response of each system are
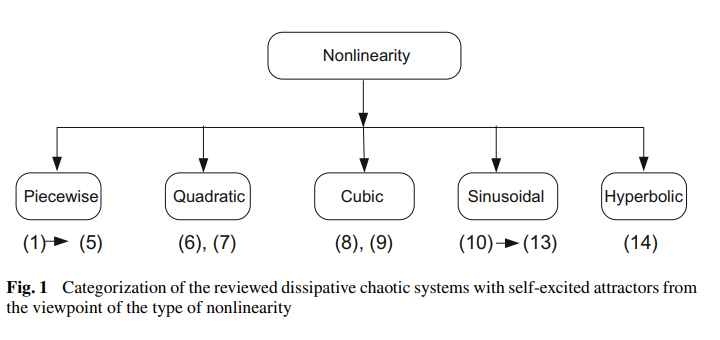
Self-excited attractors in jerk systems: Overview and numerical investigation of chaos production
Chaos theory has attracted the interest of the scientific community because of its broad range of applications, such as in secure communications, cryptography or modeling multi-disciplinary phenomena. Continuous flows, which are expressed in terms of ordinary differential equations, can have numerous types of post transient solutions. Reporting when these systems of differential equations exhibit chaos represents a rich research field. A self-excited chaotic attractor can be detected through a numerical method in which a trajectory starting from a point on the unstable manifold in the
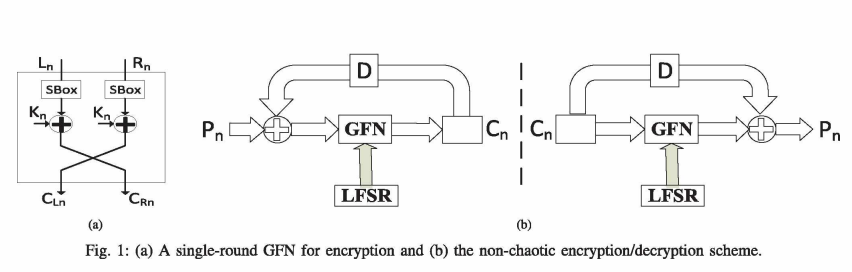
Security and Efficiency of Feistel Networks Versus Discrete Chaos for Lightweight Speech Encryption
This paper compares examples of non-chaotic and chaotic ciphers from the viewpoint of their suitability for speech encryption, especially in real-time and lightweight cipher systems. The non-chaotic encryption scheme depends on a modified Generalized Feistel Network (GFN), Linear Feedback Shift Register (LFSR) and Substitution Boxes (S-Boxes). The chaotic encryption scheme utilizes a generalized modified tent map with multiple modes of operation. The security and efficiency of both schemes are analyzed using the perceptual tests: time waveform and spectrogram; the statistical tests: histogram
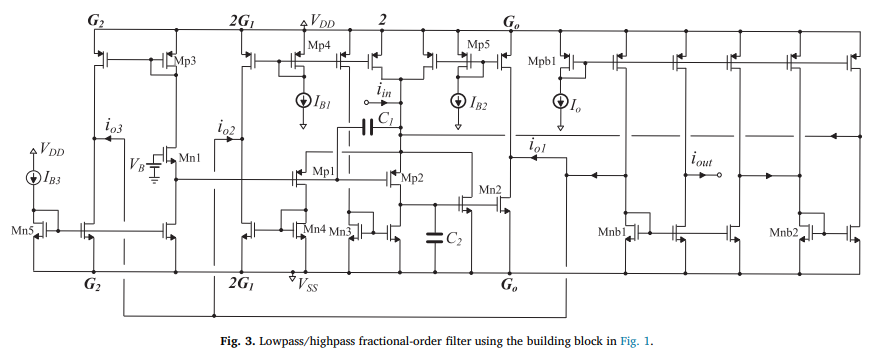
Design and application examples of CMOS fractional-order differentiators and integrators
Reduced complexity CMOS fractional-order differentiator and integrator building blocks are introduced in this work, based on 2 nd -order integer-order transfer function approximations. These blocks are then used for implementing fractional-order filters as well as a Leaky-Integrate-and-Fire Mihalas-Niebur neuron model. Cascading 1 st and 2 nd -order blocks to obtain 5 th -order integer-order transfer functions, improved bandwidth of approximation accuracy is achieved. Furthermore, the realization of fractional-order capacitor and inductor emulators is demonstrated. © 2018 Elsevier Ltd
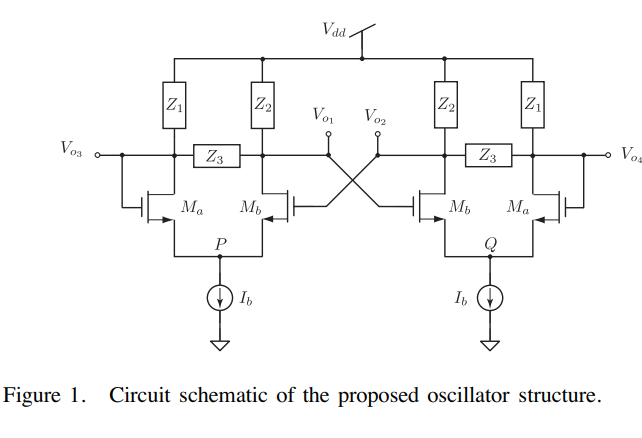
On a class of quadrature phase oscillators using differential pairs
A new class of quadrature phase oscillators based on cross-coupled differential pairs is introduced. This class contains eight possible circuits which produce four output voltages with phase differences of ±π or ±π/2, depending on the choice of output node, and does not require balanced differential-pair loads. Phase error analysis is provided along with experimental and simulation results using discrete MOS and BJT transistors as a proof of concept. © 2018 IEEE
Pagination
- Previous page ‹‹
- Page 23
- Next page ››
