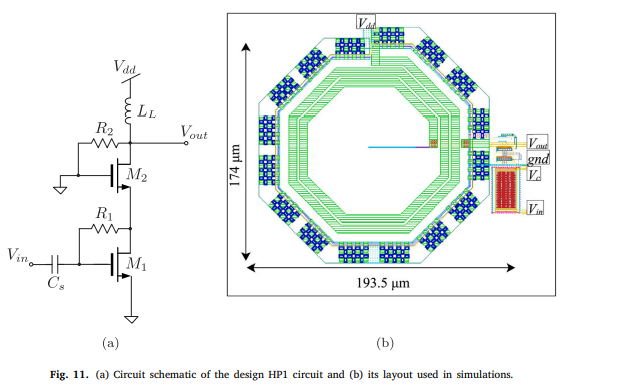
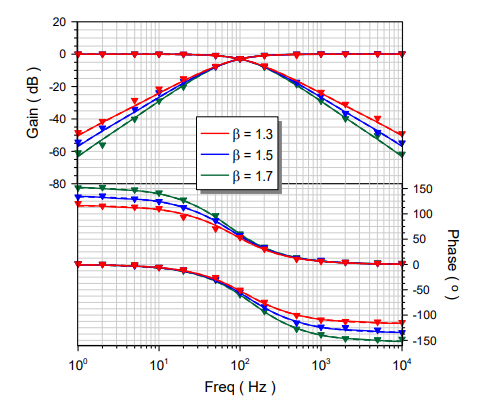
Breadcrumb
Power law filters: A new class of fractional-order filters without a fractional-order Laplacian operator
A new category of fractional-order filters, realized without employing a fractional-order Laplacian operator is introduced in this work. This can be achieved through the utilization of an efficient curve fitting method which approximates the frequency-domain behavior of the filter and transposes the fractional-order transfer function into the integer-order domain. Thus, the procedure results in a rational integer-order transfer function and its implementation is possible using conventional integer-order realization techniques. Therefore, there is no need for fractional-order elements to realize this class of filters. Design examples of this new kind of filters are presented with the derived simulation and experimental results confirming their correct performance. © 2020 Elsevier GmbH