Comparison between three approximation methods on oscillator circuits

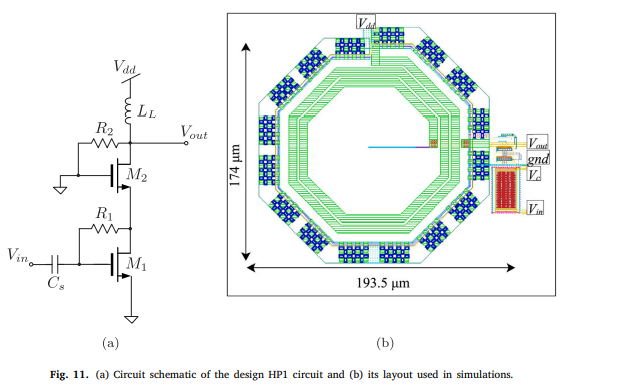
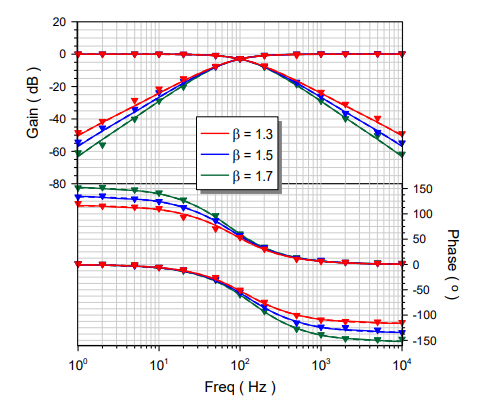
The promising capabilities of fractional-order devices challenge researchers to find a way to build it physically. Approximating the Laplacian operator sα can pave the way to emulate the fractional-order devices till its off-the-shelf appearance. This paper introduces three approximations of the Laplacian operator sα: Oustaloup, Matsuda, and Valsa by comparing their behaviors through two types of oscillator circuits. The first two are well-established approximations and the latter is proposed for the first time by converting its model network to an integer polynomial approximation of the fractional operator sα. In addition to that, three emulators for the fractional-order capacitor are introduced based on Foster-I, Foster-II, and Cauer-I techniques. The Wien-bridge family and the phase-shift oscillators are chosen to be examples of two and three fractional-order elements circuits, respectively. The approximation comparison is held through the oscillators based on oscillation condition and frequency. Also, a comparison between the circuit's behavior with three approximations and the exact solution is provided to investigate which approximation has the lowest error. The sensitivity of approximations to emulators’ circuit components is investigated through Monte Carlo analysis. The effects of 5% and 10% uniform random deviation in the emulators’ circuit components are investigated. Numerical simulations using MATLAB and Spice simulations for the two oscillators are provided. Also, some cases are validated experimentally. © 2018 Elsevier Ltd